Matematické Fórum

Aha, tak abych vysvětlil ten svůj postup s nulou:

Pokud nechci počítat limity (které jsou sice triviální, ale člověk bývá lenivý), tak se podívám, zda se grafy neliší zásadně v nějakém bodě. Pokud spočítám funkční hodnotu té funkce v tom bodě, mohu ihned vyeliminovat nějaké grafy. V tomto případě vyeliminuji všechny až na jeden.

Můj druhý postup je též takto intuitivní — když vidím, že sčítám dvě záporné hodnoty, tak se nikdy nedostanu nad osu x, takže opět dostávám jen jediný graf.

↑ Volter22:Kde si vzal že sjou to dve kladne hodnoty? Jak ta funkce bude vypadat v bodě ???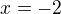

Btw u těchdle TRIAlovejch příkladů je vždycky důležitý se zamyslet... zvlášť u poznejte z grafu nebo jak přesně se to jmenuje... u konkretne tohoto prikladu asi v 99% příkladů pomůže bod 0 a limity v 1, -1

EDIT... v tomhle případě třeba ještě derivace v nule... Vždycky zkus aplikovat ty základní poznatky.. nechtějí po tobě složité výpočty, ale přemýšlení a aplikování základních poznatků (spojitost, derivace, limita)

Aha....

Takže pokud dosadíš nulu do předpisu, tak dostaneš funkční hodnotu v bodě 0... A to je hodnota toho bodu na y...

Pokud tam tedy dosadíš nulu, dostaneš nulu... to znamená, že bod x=0 se tou funkcí zobrazí na y=0... tudíž bod [0,0] musí být v tom grafu... Takže ten graf musí procházet počátkem... Doufám, že je to jasnější...

Samozřejmě se dá rozhodnout jenom z těch limit... ale tím, že si třeba určíš tu hodnotu v nule, tak si zúžíš výběr...

derivace... tady už se mi to nechce rozepisovat... Takže polozím otázku... Co určuje derivace?


BTW... 0 nedosazuješ do x ale buď do f(x) nebo ZA x dosadíš nulu... Jenom takovy slovíčkaření, ale jestli půjdeš k Matasovi, tak je schopnej tě sežrat... Pokud k Cibulkovi nebo Holubový tak asi v pohodě... popřípadě Čepička :-)

Hm hm hm...

Tak... Taky je tady dulezity rozhodnout o limite zleva a zprava... Nevim jestli se tu tu nekde výš řešilo... Takže pokud si určíš limity zleva a zprava tak muzes dostat vzdy jen jednu moznost... ty priklady jsou tak koncipovany...

Dobře, to co jsi řekl o derivaci platí, ale asi nám to nepomůže... důležité by bylo se zamyslet nad tím, že určuje směrnici tečny k funkci v daném bodě....

Derivace v bodě 0 je

Zkus si to spočíst...

Co nám to říká o tečně o obrázku? Nebo aspoň o monotonii té funkce? Ty dvě věci spolu velmi uzce souvisí, zkus si to rozmyslet... I jako přípravu ke zkoušce, kde taková otázka může klidně padnout...


BTW u případu (3) ani jedna limita (v 1 a -1) neexistuje... Proč?


BTW 2... Ještě je možnost, že půjdeš na konzultaci k některému z vyučujících, kteří by ti popřípadě pomohli s nějakými příklady..

BTW 3... Nebo existuje spousta lidí, kteří jsou ochotní za nějakou úplatu danou problematiku doucít, nebo třeba jen vysvětlit příklady... Popřípadě určitě máš nějakého chytřejsího spolužáka, který by ti pomohl...

BTW 4... pokud jdeš na třetí termín zkoušky, tak ani test napsat nemusíš a půjdeš k ústní...

EDIT:

Záporná derivace značí klesající funkci.  Jestli si to nevymyslel popřípadě nevyčetl... takže z toho taky můžeš vycházet. A budou tam příklady, kdy budeš moct vyjít jen z té derivace někdy i z její velikosti...

↑ Volter22:
Ano ano... a pokud je derivace 0, tak se jedná o bod podezřelý z extrému...

Jestli chceš, můžeš mi napsat na ICQ. Když budu mít čas, tak se ti pokusím odpovědět. TRIALové příklady by neměli být problém...
299488574