Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 07. 2010 13:06
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
komplexní čísla 3.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#3 21. 07. 2010 14:22 — Editoval Rumburak (22. 07. 2010 10:16)
Re: komplexní čísla 3.
A jak zní zadání ? Jde o binomické rovnice, které se mají vyřešit ?
Pokud ano, ukážeme si to na té rovnici 2. Nejprve její pravou stranu  převedeme do goniometrického (neboli polárního) tvaru,
převedeme do goniometrického (neboli polárního) tvaru,
tím rovnice dostane tvar
(1)  .
.
V goniomerickém tvaru vyjádříme i neznámou  , což můžeme provést bez dalších diskusí, neboť je zřejmé, že číslo 0 , které jako jediné komplexní číslo
, což můžeme provést bez dalších diskusí, neboť je zřejmé, že číslo 0 , které jako jediné komplexní číslo
nemá gonometrický tvar, kořenem naší rovnice není. Takže  , kde
, kde  ,
,  jsou nyní již reálné neznámé.
jsou nyní již reálné neznámé.
Dle Moivreovy poučky provedeme umocnění neznámé  :
:  a toto dosadíme do (1). Obdržíme tak rovnici
a toto dosadíme do (1). Obdržíme tak rovnici
 .
.
Z ní vyplývají dvě věci:
(a)  , neboli
, neboli ![kopírovat do textarea $\rho\,=\,\sqrt[8]{2}$](/mathtex/c8/c8a7dfd2a9cb9ed338a7f104383abd87.gif) (podle předpokladu, že
(podle předpokladu, že  ) ,
) ,
(b)  , kde
, kde  je zvolené celé číslo . Odtud
je zvolené celé číslo . Odtud  .
.
Podmínka  vede k nutnosti omezit se na
vede k nutnosti omezit se na  . Pro další celočíselné hodnoty indexu
. Pro další celočíselné hodnoty indexu  bychom už žádné další kořeny
bychom už žádné další kořeny
rovnice (1) stejně nedostali, neboť pro libovolné celé číslo  je
je 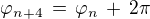 a
a  je periodou funkcí sin, cos , takže
je periodou funkcí sin, cos , takže
 .
.
Jedinými kořeny rovnice (1) jsou tedy komplexní čísla
![kopírovat do textarea $r_k \,:=\,\sqrt[8]{2}\,\(\cos \,\varphi_k \,+\,i\,\sin \,\varphi_k \)\,=\,\sqrt[8]{2}\,\(\cos \,\(\frac{3}{16}\pi \,+\,k\cdot \frac{1}{2}\pi \) \,+\,i\,\sin \,\(\frac{3}{16}\pi \,+\,k\cdot \frac{1}{2}\pi \) \)$](/mathtex/e6/e64387b63d678d892e467c4865a4cf61.gif) ,
,  .
.
*********
Ta prvá rovnice by se řešila obdobně, avšak v jejím zadání je drobný problém: jak definovat druhou odmocninu z imaginárního čísla ?
Pokud definici (která není triviální a jsou k ní různé přístupy) máme, tak ji použijeme k vyjádření čísla  (potřebujeme jeho
(potřebujeme jeho
goniometrický tvar).
Nemáme-li definici pro  , můžeme to obejít tím, že rovnici umocníme na druhou a místo ní pak řešíme rovnici
, můžeme to obejít tím, že rovnici umocníme na druhou a místo ní pak řešíme rovnici  .
.
Offline
#4 21. 07. 2010 14:36 — Editoval Lucinecka88 (21. 07. 2010 14:51)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 3.
↑ Krezz:
Toto je ta věta,ale nevím co do čeho dosadit.
↑ Rumburak:
Děkuji,ale nějak jsem to nepobrala. Zadání je vyřeště.
Offline
#5 21. 07. 2010 14:43
#6 21. 07. 2010 16:54
#7 21. 07. 2010 17:21
Re: komplexní čísla 3.
↑ Lucinecka88:
Takže pravá strana je nikoliv  , ale
, ale  (tj.
(tj.  už ne pod odmocninou) ? To je ovšem něco podstatně jiného.
už ne pod odmocninou) ? To je ovšem něco podstatně jiného.
Potom převodem na gon. tvar dostaneme  , kde
, kde 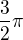 je 270 stupňů, jak i Tobě vyšlo.
je 270 stupňů, jak i Tobě vyšlo.
Teď ještě zbývá vyřešit rovnici  .
.
Jak ? V mém předchozím příspěvku je to popsáno, Nepodléhej panice a zkus si to prostudovat a promyslet, není to nic těžkého.
Zítra případně zodpovím nějaký doplňující dotaz, dnes už tu musím končit.
Offline
#8 22. 07. 2010 10:12
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 3.
↑ Rumburak:
Ahoj udělala jsem ještě toto. 
To je už výsledek nebo ještě něco dál? Děkuju za pomoc.
Offline
#9 22. 07. 2010 10:33 — Editoval zdenek1 (22. 07. 2010 10:35)
Re: komplexní čísla 3.
↑ Lucinecka88:
od pátého řádku je to špatně.
má to být takto.
![kopírovat do textarea $r_k=\sqrt[6]3\left(\cos\frac{270+k\cdot360}6+i\sin\frac{270+k\cdot360}6\right)$](/mathtex/d0/d074ed8aa6daa44d84153b32b5987544.gif) ,
, 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 22. 07. 2010 10:40
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 3.
↑ zdenek1:
Proč to má být takto? Děkuji za vysvětlení.
Offline
#11 22. 07. 2010 11:10 — Editoval Rumburak (22. 07. 2010 11:12)
Re: komplexní čísla 3.
↑ Lucinecka88:
Ahoj, rád bych Ti pomohl, ale z Tvých příspěvků příliš nechápu, jaké je vlastně zadání o co se tedy máme snažit,
navíc tam máš dvě nesrovnalosti:
1) V prvním řádku píšeš  .
.
Druhá z těchto rovností, tj. rovnost  , kde
, kde  JE ještě POD odmocninou, je CHYBNÁ, správná by byla rovnost
JE ještě POD odmocninou, je CHYBNÁ, správná by byla rovnost , kde
, kde  už NENÍ POD odmocninou, což je něco ZCELA JINÉHO. Jako pravděpodobnější z pohledu SŠ
už NENÍ POD odmocninou, což je něco ZCELA JINÉHO. Jako pravděpodobnější z pohledu SŠ
matematiky mi připadá, že ta DRUHÁ varianta je správná, ale měla bys to potom správně zapisovat.
2) Je-li tedy správná ta druhá varianta, pak můžeme v úpravách pravé strany (jejím převodem do gon. tvaru) pokračovat :
 , což je správně.
, což je správně.
Pak ale nechápu, proč na pátém řádku máš místo toho , kde
, kde  už je jen v první mocnině.
už je jen v první mocnině.
Zkus se vrátit na úplný začátek a přesně zformuluj zadání úlohy. Co se vlastně má řešit ?
A) Mají se najít kořeny binomické rovnice  (nebo snad rovnice
(nebo snad rovnice 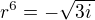 ?) ,
?) ,
nebo
B) má se číslo  (nebo snad
(nebo snad  ) umocnit na šestou pomocí Moivreovy věty,
) umocnit na šestou pomocí Moivreovy věty,
jak by naznačoval Tvůj postup od 5. řádku dále ?
Ve hře jsou tedy celkem dvě různé úlohy, navíc ve dvou různých variantách, a připadá mi, že Ti zatím není jasné, které je ta pravá :-)
(nevysmívám se, pouze usmívám).
Offline
#12 22. 07. 2010 11:24
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 3.
↑ Rumburak:
Zadání úlohy je řešte: 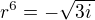
Offline
#13 22. 07. 2010 11:46 — Editoval Rumburak (22. 07. 2010 16:56)
Re: komplexní čísla 3.
↑ Lucinecka88:
OK. Tedy jde o nalezení kořenů binomické rovnice 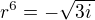 , jak se od začátku jevilo mně i kolegovi Zdeňkovi (viz ↑ zdenek1:).
, jak se od začátku jevilo mně i kolegovi Zdeňkovi (viz ↑ zdenek1:).
Trváš na tom, že imaginární jednotka je POD odmocninou ? Pokud ano, tak si vzpomeň, jak jste si definovali druhou odmocninu z komplexního čísla
nebo aspoň druhou odmocninu z imaginární jednotky. Možnost by byla
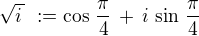 (tzv. hlavní větev druhé odmocniny),
(tzv. hlavní větev druhé odmocniny),
takže rovnice 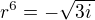 přejde na
přejde na
 .
.
Dále je třeba postupovat analogicky jako v mém prvním příspěvku ↑ Rumburak: , kde je to podrobně vysvětleno.
K mé otázce, které místo Ti není jasné (↑ Rumburak:), ses nakonec nevyjádřila, tak předpokládám, že už bylo pochopeno ...
Offline
#14 22. 07. 2010 11:59
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 3.
Děkuji oběma už to snad chápu a nějak to udělám.
Offline


