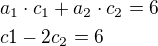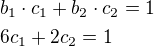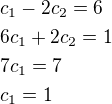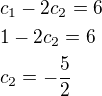Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 08. 2010 20:34
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
vektorová algebra
Ahoj, mám jeden úkol a nevím si rady. Můžete mě prosím nějak nakopnout? Děkuji
Kosočverec ABCD má vrcholy A=[0,0],B=[10,0],C=[16,c]. Určete souřadnice vektoru AC, AD, BD.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#6 17. 08. 2010 21:24 — Editoval jarrro (17. 08. 2010 21:27)
Re: vektorová algebra
↑ Lucinecka88:nie ![kopírovat do textarea $C=\left[16;\pm8\right]$](/mathtex/54/54da2429f1f436dd5fbb8db3e9a320dd.gif) resp. len
resp. len![kopírovat do textarea $\left[16;8\right]$](/mathtex/9c/9ce3d9f72f3026ea761f4af703263044.gif) aby sa zachovalo štandardné poradie značenia a jednoznačnosť
aby sa zachovalo štandardné poradie značenia a jednoznačnosť
úlohy
MATH IS THE BEST!!!
Offline
#7 18. 08. 2010 09:55 — Editoval Lucinecka88 (18. 08. 2010 10:10)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: vektorová algebra
↑ jarrro:
Tak to nevím jak jsi udělal, protože když jsem to počítala podle tebe (|AB|=|BC|), tak mi vyšlo c=4. Už vím, udělala jsem chybu.
Offline
#8 18. 08. 2010 10:16
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: vektorová algebra
Jenom bych se ještě chtěla zeptat, jak mám vypočítat vrchol D, abych mohla vypočítat ty vektory? Děkuji za pomoc.
Offline
#9 18. 08. 2010 10:28 — Editoval Cheop (18. 08. 2010 10:30)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: vektorová algebra
↑ Lucinecka88:
Délka strany kosočtverce je 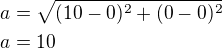 - vzdálenost AB
- vzdálenost AB
Podle obrázku platí: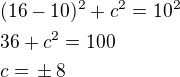
Dále platí: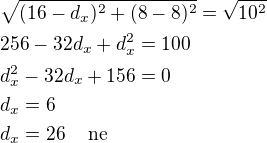
Obrázek:
Nikdo není dokonalý
Offline
#10 18. 08. 2010 10:36
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: vektorová algebra
↑ Cheop:
Dobrá. Kde jsi prosímo vzal y souřadnici v D, že je 8?
Offline
#11 18. 08. 2010 11:17 — Editoval Cheop (18. 08. 2010 11:43)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: vektorová algebra
↑ Lucinecka88:
Protože je to kosočtverec a y-ové souřadnice bodů A,B jsou stejné(0) a y-ovou souřadnici bodu C jsme spočítali jako 8,
pak y-ová souřadnice bodu D musí být také 8
Strana AB musí být rovnoběžná s CD
Nikdo není dokonalý
Offline
#12 18. 08. 2010 14:33
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: vektorová algebra
↑ Cheop:
Děkuji, už to mám hotový.
Mám další problém s tímto příkladem. Vůbec nevím jak to mám udělat. Děkuji za pomoc.
Zadání: Určete souřadnice vektoru c pod šipkou=(c1, c2)
a) vektor a x vektor c = 6 vektor a = (1,-2)
vektor b x vektor c = 1 vektor b = (6,2)
Offline
#13 18. 08. 2010 14:43
Re: vektorová algebra
↑ Lucinecka88:
Podmínky
vektor a x vektor c = 6
vektor b x vektor c = 1
zapíšeme pomocí rovnic s neznámými c1, c2 a vzniklou soustavu vyřešíme.
Offline
#14 18. 08. 2010 14:46
#15 18. 08. 2010 15:02
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: vektorová algebra
↑ Cheop:
Děkuji, toto mně nenapadlo. Strašně moc děkuji.
Offline
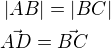
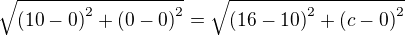 a vektor AD je rovný vektoru BC
a vektor AD je rovný vektoru BC