Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 09. 2010 21:47
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Rekurentní rovnice, počet koster
Nechť je funkce t(n,k) dána vztahem (n,k přirozená čísla, n>=k):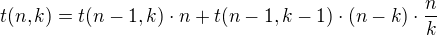 ,
,
počáteční podmínky jsou dány: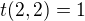
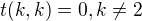
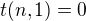
(Význam t(n,k): jedná se o počet stromů (koster) na n vrcholech majících právě k vrcholů stupně 1)
Počet stromů na n vrcholech je tedy dán hodnotou b(n), kde: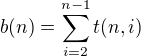
Odvoďte explicitní vzorec pro b(n) jakožto funkci proměnné n. (Jak známo, je 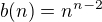 .)
.)
Úlohu jsem zařadil do této kategorie, protože řešení této rovnice je zejména problém algebraický - grafový pohled by však také mohl pomoci...
Pozn: Hint nemám, zde jsem se zasekl. :-)
"Máte úhel beta." "No to nemám."
Offline