Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Binomická čísla III. (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 10. 2010 11:58 — Editoval Pavel (09. 10. 2010 13:11)
Binomická čísla III.
Inspirován úlohou Binomická čísla II. uvádím další:
Nechť 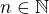 . Najděte součet
. Najděte součet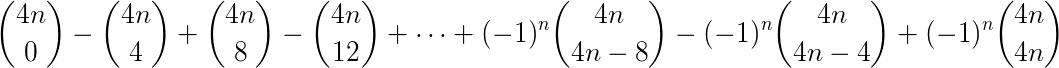 .
.
HINT :
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
- (téma jako vyřešené označil(a) Pavel)
#2 29. 10. 2010 20:01 — Editoval andrew (29. 10. 2010 20:05)
Re: Binomická čísla III.
Offline
#3 23. 12. 2010 19:22 — Editoval Pavel (23. 12. 2010 19:23)
Re: Binomická čísla III.
↑ andrew:
Po drahné době se opět dostávám k tomuto problému.
Bohužel to není dobře. Neplatí totiž ![kopírovat do textarea $\Re\Big[(1+ \sqrt{\mathrm{i}})^{4n}\Big] = {4n \choose 0} - {4n \choose 4} + {4n \choose 8} - {4n \choose 12} + \cdots +(-1)^n {4n \choose 4n}$](/mathtex/61/61bc87a4fff0b89b87d8ae41fdd208d0.gif)
Stačí vzít druhý člen binomického rozvoje 

a je zřejmé, že i v něm se objevuje nenulová reálná složka  , která ve výše uvedené identitě chybí.
, která ve výše uvedené identitě chybí.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 23. 12. 2010 22:18 — Editoval Pavel (23. 12. 2010 22:24)
Re: Binomická čísla III.
Řešení:
Nechť 
je kořenem rovnice  . Pak všechny kořeny této rovnice je možné vyjádřit ve tvaru
. Pak všechny kořeny této rovnice je možné vyjádřit ve tvaru  .
.
Sečtěme binomické rozvoje![kopírovat do textarea $ (1+\varepsilon)^{4n}=\binom{4n}{0}\varepsilon^0+\binom{4n}{1}\varepsilon+\binom{4n}{2}\varepsilon^2+\binom{4n}{3}\varepsilon^3+\dots+\binom{4n}{4n-3}\varepsilon^{4n-3}+\binom{4n}{4n-2}\varepsilon^{4n-2}+\binom{4n}{4n-1}\varepsilon^{4n-1}+\binom{4n}{4n}\varepsilon^{4n}\nl (1-\varepsilon)^{4n}=\binom{4n}{0}\varepsilon^0-\binom{4n}{1}\varepsilon+\binom{4n}{2}\varepsilon^2-\binom{4n}{3}\varepsilon^3+\dots-\binom{4n}{4n-3}\varepsilon^{4n-3}+\binom{4n}{4n-2}\varepsilon^{4n-2}-\binom{4n}{4n-1}\varepsilon^{4n-1}+\binom{4n}{4n}\varepsilon^{4n}\nl \nl (1+\varepsilon)^{4n}+(1-\varepsilon)^{4n}=2\left[\binom{4n}{0}\varepsilon^0+\binom{4n}{2}\varepsilon^2+\binom{4n}{4}\varepsilon^4+\binom{4n}{6}\varepsilon^6+\dots+\binom{4n}{4n-6}\varepsilon^{4n-6}+\binom{4n}{4n-4}\varepsilon^{4n-4}+\binom{4n}{4n-2}\varepsilon^{4n-2}+\binom{4n}{4n}\varepsilon^{4n}\right] $](/mathtex/93/93dff3fe1e145c384cb53d4dd434af4e.gif)
![kopírovat do textarea $ (1+\varepsilon^3)^{4n}=\binom{4n}{0}\varepsilon^0+\binom{4n}{1}\varepsilon^3+\binom{4n}{2}\varepsilon^6+\binom{4n}{3}\varepsilon^9+\dots+\binom{4n}{4n-3}\varepsilon^{12n-9}+\binom{4n}{4n-2}\varepsilon^{12n-6}+\binom{4n}{4n-1}\varepsilon^{12n-3}+\binom{4n}{4n}\varepsilon^{12n}\nl (1-\varepsilon^3)^{4n}=\binom{4n}{0}\varepsilon^0-\binom{4n}{1}\varepsilon^3+\binom{4n}{2}\varepsilon^6-\binom{4n}{3}\varepsilon^9+\dots-\binom{4n}{4n-3}\varepsilon^{12n-9}+\binom{4n}{4n-2}\varepsilon^{12n-6}-\binom{4n}{4n-1}\varepsilon^{12n-3}+\binom{4n}{4n}\varepsilon^{12n}\nl \nl (1+\varepsilon^3)^{4n}+(1-\varepsilon^3)^{4n}=2\left[\binom{4n}{0}\varepsilon^0+\binom{4n}{2}\varepsilon^6+\binom{4n}{4}\varepsilon^{12}+\dots+\binom{4n}{4n-4}\varepsilon^{12n-12}+\binom{4n}{4n-2}\varepsilon^{12n-6}+\binom{4n}{4n}\varepsilon^{12n}\right] $](/mathtex/ab/ab90f0c09aaf9c1389ceb208bd13dd86.gif)
Oba součty sečtěme![kopírovat do textarea $ (1+\varepsilon)^{4n}+(1-\varepsilon)^{4n}+(1+\varepsilon^3)^{4n}+(1-\varepsilon^3)^{4n}=2\left[\binom{4n}{0}(\varepsilon^0+\varepsilon^0)+\binom{4n}{2}(\varepsilon^2+\varepsilon^6)+\binom{4n}{4}(\varepsilon^4+\varepsilon^{12})+\binom{4n}{6}(\varepsilon^6+\varepsilon^{18})+\dots+\right.\nl\left.+\binom{4n}{4n-6}(\varepsilon^{4n-6}+\varepsilon^{12n-18})+\binom{4n}{4n-4}(\varepsilon^{4n-4}+\varepsilon^{12n-12})+\binom{4n}{4n-2}(\varepsilon^{4n-2}+\varepsilon^{12n-6})+\binom{4n}{4n}(\varepsilon^{4n}+\varepsilon^{12n})\right] $](/mathtex/a4/a4870eb89b6cef30c426e1c852f468f9.gif)
Součty mocnin kořene  lze zjednodušit podle následujícího pravidla:
lze zjednodušit podle následujícího pravidla:![kopírovat do textarea $ \varepsilon^{4n+2}+\varepsilon^{3(4n+2)}=\varepsilon^{4n+2}+\varepsilon^{12n+6}=\varepsilon^{4n+2}(1+\varepsilon^{8n+4})=\varepsilon^{4n+2}[1+(\varepsilon^4)^{2n+1}]=\varepsilon^{4n+2}[1+(-1)^{2n+1}]=0,\quad\forall n\in\mathbb{N},\nl \varepsilon^{4n}+\varepsilon^{3(4n)}=\varepsilon^{4n}+\varepsilon^{12n}=\varepsilon^{4n}(1+\varepsilon^{8n})=(\varepsilon^4)^n[1+(\varepsilon^8)^n]=(-1)^n(1+1^n)=2\cdot(-1)^n,\quad\forall n\in\mathbb{N}. $](/mathtex/35/35e632e929b296b75a03d1f8e46a1903.gif)
Pak tedy platí![kopírovat do textarea $ (1+\varepsilon)^{4n}+(1-\varepsilon)^{4n}+(1+\varepsilon^3)^{4n}+(1-\varepsilon^3)^{4n}=\ldots=2\biggl[2\binom{4n}{0}-2\binom{4n}{4}+2\binom{4n}{8}-2\binom{4n}{12}+\dots+\nl +2\cdot(-1)^{n-3}\binom{4n}{4n-12}+2\cdot(-1)^{n-2}\binom{4n}{4n-8}+2\cdot(-1)^{n-1}\binom{4n}{4n-4}+2\cdot(-1)^n\binom{4n}{4n}\biggr]=\nl =4\left[\binom{4n}{0}-\binom{4n}{4}+\binom{4n}{8}-\binom{4n}{12}+\dots+(-1)^{n-3}\binom{4n}{4n-12}+(-1)^{n-2}\binom{4n}{4n-8}+(-1)^{n-1}\binom{4n}{4n-4}+(-1)^n\binom{4n}{4n}\right] $](/mathtex/5d/5def1fb155bb69fe71cb5d02b8f29ac4.gif)
Odtud určíme hledaný součet![kopírovat do textarea $ \binom{4n}{0}-\binom{4n}{4}+\binom{4n}{8}-\binom{4n}{12}+\dots+(-1)^{n-3}\binom{4n}{4n-12}+(-1)^{n-2}\binom{4n}{4n-8}+(-1)^{n-1}\binom{4n}{4n-4}+(-1)^n\binom{4n}{4n}=\nl=\frac 14\,\left[(1+\varepsilon)^{4n}+(1-\varepsilon)^{4n}+(1+\varepsilon^3)^{4n}+(1-\varepsilon^3)^{4n}\right]=\frac 14\left\{\left[\sqrt{2+\sqrt{2}}\,\left(\cos\frac{\pi}{8}+i\sin\frac{\pi}{8}\right)\right]^{4n}+\left[\sqrt{2-\sqrt{2}}\,\left(\cos\left(-\frac{3\pi}{8}\right)+i\sin\left(-\frac{3\pi}{8}\right)\right)\right]^{4n}+\right.\nl\left.+\left[\sqrt{2-\sqrt{2}}\,\left(\cos\frac{3\pi}{8}+i\sin\frac{3\pi}{8}\right)\right]^{4n}+\left[\sqrt{2+\sqrt{2}}\,\left(\cos\left(-\frac{\pi}{8}\right)+i\sin\left(-\frac{\pi}{8}\right)\right)\right]^{4n}\right\}=\nl \frac 14\left[(2+\sqrt{2})^{2n}\,\left(\cos\frac{\pi n}{2}+i\sin\frac{\pi n}{2}\right)+(2-\sqrt{2})^{2n}\,\left(\cos\frac{3\pi n}{2}-i\sin\frac{3\pi n}{2}\right)+(2-\sqrt{2})^{2n}\,\left(\cos\frac{3\pi n}{2}+i\sin\frac{3\pi n}{2}\right)+(2+\sqrt{2})^{2n}\,\left(\cos\frac{\pi n}{2}-i\sin\frac{\pi n}{2}\right)\right]=\nl \frac 14\left[2(2+\sqrt{2})^{2n}\,\cos\frac{\pi n}{2}+2(2-\sqrt{2})^{2n}\,\cos\frac{3\pi n}{2}\right]=\frac 12\left[(2+\sqrt{2})^{2n}\,\cos\frac{\pi n}{2}+(2-\sqrt{2})^{2n}\,\cos\frac{3\pi n}{2}\right]=\nl=\frac 12\left[2^n(\sqrt{2}+1)^{2n}\,\cos\frac{\pi n}{2}+2^n(\sqrt{2}-1)^{2n}\,\cos\frac{3\pi n}{2}\right]=2^{n-1}\left[(\sqrt{2}+1)^{2n}\,\cos\frac{\pi n}{2}+(\sqrt{2}-1)^{2n}\,\cos\frac{3\pi n}{2}\right]. $](/mathtex/ba/ba128dc11d116484db89f8941152d3fc.gif)
Výsledek bude záviset na tom, zda je  sudé nebo liché.
sudé nebo liché.![kopírovat do textarea $ \binom{4n}{0}-\binom{4n}{4}+\dots+(-1)^{n-1}\binom{4n}{4n-4}+(-1)^n\binom{4n}{4n}= \begin{cases} 0,\qquad n=2k+1,\nl (-1)^{\frac n2}\,2^{n-1}\left[(\sqrt{2}+1)^{2n}+(\sqrt{2}-1)^{2n}\right],\quad n=2k,\ k\in\mathbb{N}. \end{cases} $](/mathtex/de/decc787605c9d01d28bbf3fb69702fee.gif)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Binomická čísla III. (TOTO TÉMA JE VYŘEŠENÉ)

 , kde
, kde ![kopírovat do textarea $\sum_{k=0}^{n} (-1)^k{4n \choose 4k} = \Re\Big[(1+ \sqrt{\mathrm{i}})^{4n}\Big] = {4n \choose 0} - {4n \choose 4} + {4n \choose 8} - {4n \choose 12} + \cdots +(-1)^n {4n \choose 4n} = $](/mathtex/cf/cf6182e22d27aa8550347f6ad7396010.gif)
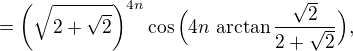 kde
kde ![kopírovat do textarea $\Re[.] $](/mathtex/ae/ae1e82d146a3dd9df12e3b50644998c6.gif) je realna cast komplexniho cisla.
je realna cast komplexniho cisla.