Matematické Fórum

Chanzy · 25. 10. 2010 06:37

Zdravím, dostali jsme ve škole za úkol cvičení 3.4 - 3.6 a já vůbec nevím jak mám tyto limity upravit, aby platily. Prosím o pomoc, nechci, aby jste mi počítali úkol, jen prosím o "nakopnutí" jak s tím začít, moc děkuji

jelena · 25. 10. 2010 09:51

↑ Chanzy:

Zdravím,

užitečný Rychlokurz od kolegy Ondřeje.

3.4) úprava pomocí užitečných vzorců a rozkladu na součin.

3.5) použití goniometrických vzorců za účelem dosažení v zápisu výrazu (sin(x))/x pro x k 0.

3.6) kombinace předchozích doporučení.

Nejdůležitější jsou úpravy výrazů. Ať se vede.

Chanzy · 25. 10. 2010 13:22

ať se snažím sebevíc, stále mi vychází jen jeden příklad, mohl by mi to tu ukázat na 1 příkladu z každého cvičení? Děkuji

jelena · 25. 10. 2010 14:16

↑ Chanzy: teď (ani do pozdních věčerních hodin bych čas neměla), zkus projit příklady od kolegy da.backer v posledním období v tématech VŠ.

Hodně vzorů nebo nápověd je vyřešeno/uvedeno zde (v adresové řádce je třeba změnit číslo kapitoly). Online nástroj pro kontrolu - pomoci takového vstupu do Wolfram (děkuji autorům) by to neměl byt problém, v Show steps jsou po rozkliknutí jednotlivé kroky. Ve "zkusit online" můžeš vložit své zadání podle vzoru.

Opravdu jde hlavně o úpravy výrazů, ne tak o limity. Zkus sem vyfotit (nascanovat) své úpravy. Děkuji.

Chanzy · 25. 10. 2010 14:53

A nenašel by se tu někdo jiný, kdo by mi pomohl?

jelena · 25. 10. 2010 17:41

↑ Chanzy:

Nejsem jediná - ale to vyžaduje hodně času - snad od každého, ale nevím (ohledně času - mluvím jen za sebe) - zde jsem naznačila 1. krok úpravy: zkus zadání po zadání.

3.4) a, b rozšíření zlomku do vzorce
3.4) c) rozklad kvadratického trojčlenu na činitele
3.4) d) rozklad na součin pomoci rozpisu 2x=x+x a potom vytknutí po dvojicích

3.5) goniometrické vzorce, cíl - mít "sin(x)/x pro x k 0.

3.6) podobně.

Dá se pomáhat úloha po úloze nebo pokud vídím, kde máš problém. Nevím, jak ovládáš úpravu výrazů - nic jiného v tom není. Z pohledu limit - skoro všude je neurčitý výraz 0/0.

Napíš si zadání po zadání na papír a scan nebo do Malování (bude jasné, co je problém). Děkuji.

halogan · 25. 10. 2010 19:05

Asi bude potřeba ale vědět, co používáte na hodinách, abychom mohli zvolit správné nástroje:

1) Umíš rozšiřovat?
2) Umíš upravovat na a^2 - b^2?
3) Umíš upravovat na a^n - b^n?
4) Umíš upravovat goniometrické funkce (hlavně z tg/cotg na sin a cos, případně dvojité úhly)?
5) Znáš nějaké tabulkové limity?
6) Jsi ochoten používat selský rozum při počítání limit? (to je myšleno naprosto vážně)
7) Umíš dělit polynomy?

Každý dotaz se týká nějakých limit.

---

Nebudeme ti tu počítat jednu po druhé. Vyber si nějakou ukázkovou, zkus, co umíš, a my tě nějak dokopem k výsledku.

Hezký večer přeji.

Chanzy · 25. 10. 2010 20:45

vše co tu píšeš si myslím, že umím...tak třeba 3.4; c)...vím že je tam vzoreček, ale jsou tam jiné znaménka

halogan · 25. 10. 2010 20:50

↑ Chanzy:

Tak. Nějaké limitové aparáty bokem. Co umíme s kvadratickými funkcemi? Znaménka jsou v pořádku.

Chanzy · 25. 10. 2010 20:51

teď bohužel nevím nač se mě ptáš :(

halogan · 25. 10. 2010 20:53

↑ Chanzy:

No tak do toho zasáhnu trochou teorie napřed, bude to asi ku prospěchu věci:

Pokud máme v nějakém bodě nějakou spojitou funkci, tak její limita v tom bodě je její funkční hodnota. Prostě dosadíme. Pokud zkusíme dosadit, tak dostaneme 0/0, což nám moc nepomůže.

Naštěstí jsme se někdy v 7. tříde (+- pět let) učili něco o kvadratických funkcích. Víme, že mají (v R) 1, dva, nebo žádný kořen. Pokud mají 1-2 kořeny, tak je umíme nějak "složit". Uměl bys to u těchto dvou funkcí?

Chanzy · 25. 10. 2010 20:55

nejspíš ne, vadí mi tam že tam není jeden kvadratický člen, promiň, jsem asi lama

halogan · 25. 10. 2010 21:00

↑ Chanzy:

Koukáme na stejnou úlohu? 3.4 c)? Jsou tam všechny členy — kvadratický, lineární i absolutní.

Začnu jmenovatelem:

$f(x) = 3x^2 -x -2 \nl D = b^2 - 4ac = 1 + 24 = 25 \nl x_{1,2} = \frac{1 \pm 5}{6} = \frac 16 \pm \frac 56 \nl x_1 = -2/3, x_2 = 1$

A my víme, že kvadratická funkce 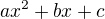$ax^2 + bx + c$ (a není rovno nule) se dvěma kořenama se dá napsat jako $a(x - x_1)(x-x_2)$ .

U nás tedy 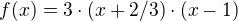$f(x) = 3\cdot (x + 2/3) \cdot (x - 1)$ .

Jasné? Co čitatel?

Chanzy · 25. 10. 2010 21:06

mě vyšli kořeny 3/2 a -8/12 ale nevím co teď

Nextland · 25. 10. 2010 21:14

-8/12 se dá ještě zkrátit.;-)
Pak napiš rovnici v součinovém tvaru (viz ↑ halogan: a výraz (6x^2-5x-6)/(3x^2-x-2) napiš pomocí součinů.

halogan · 25. 10. 2010 21:15

↑ Chanzy:

1) Taky mě tlačí čas. Už je holt taková doba.

2) Je těžké si to odvodit pro čitatele a mít v tom jasno?

3) Pokud tě tlačí čas u této limity, tak tě bude tlačit u všech. Buďto se to chceš naučit, nebo ne.

Chanzy · 25. 10. 2010 21:17

já chápu ten princip, ale mě se tu nic nezkrátí

halogan · 25. 10. 2010 21:20

↑ Chanzy:

Jak ti vyšel čitatel? Jak píše kolega — $-8/12 = -2/3$ .

Chanzy · 25. 10. 2010 21:21

6*(x+1/4)*(x-1/9)

halogan · 25. 10. 2010 21:24

↑ Chanzy:

Vždyť ti vyšly úplně jiné kořeny nahoře: ↑ Chanzy:.

Chanzy · 25. 10. 2010 21:25

ale po vydělení 6 mi vyjde toto

halogan · 25. 10. 2010 21:28

↑ Chanzy:

Ty je ale nemůžeš dělit šesti. To bys po roznásobení dostal přeci úplně jinou funkci. Prostě je nech tak, jak jsou.

Chanzy · 25. 10. 2010 21:33

jj, tak se mi tam zkrátí, ale stejně mi nevyjde výsledek podle výsledků

Chanzy · 25. 10. 2010 21:45

Mě vychází 13/5 a má vyjít 1/3 :(

halogan · 25. 10. 2010 21:47

↑ Chanzy:

Mně to podle našich postupů vyjde 13/5. Stroj říká 13/5. Jestli je ve výsledcích něco jinak, je to špatně.

Matematické Fórum

#1 25. 10. 2010 06:37

Úpravy limit

#2 25. 10. 2010 09:51

Re: Úpravy limit

#3 25. 10. 2010 13:22

Re: Úpravy limit

#4 25. 10. 2010 14:16

Re: Úpravy limit

#5 25. 10. 2010 14:53

Re: Úpravy limit

#6 25. 10. 2010 17:41

Re: Úpravy limit

#7 25. 10. 2010 19:05

Re: Úpravy limit

#8 25. 10. 2010 20:45

Re: Úpravy limit

#9 25. 10. 2010 20:50

Re: Úpravy limit

#10 25. 10. 2010 20:51

Re: Úpravy limit

#11 25. 10. 2010 20:53

Re: Úpravy limit

#12 25. 10. 2010 20:55

Re: Úpravy limit

#13 25. 10. 2010 21:00

Re: Úpravy limit

#14 25. 10. 2010 21:06

Re: Úpravy limit

#15 25. 10. 2010 21:14

Re: Úpravy limit

#16 25. 10. 2010 21:15

Re: Úpravy limit

#17 25. 10. 2010 21:17

Re: Úpravy limit

#18 25. 10. 2010 21:20

Re: Úpravy limit

#19 25. 10. 2010 21:21

Re: Úpravy limit

#20 25. 10. 2010 21:24

Re: Úpravy limit

#21 25. 10. 2010 21:25

Re: Úpravy limit

#22 25. 10. 2010 21:28

Re: Úpravy limit

#23 25. 10. 2010 21:33

Re: Úpravy limit

#24 25. 10. 2010 21:45

Re: Úpravy limit

#25 25. 10. 2010 21:47

Re: Úpravy limit

Zápatí