Matematické Fórum

mp3jj · 04. 04. 2008 16:36

Které číslo je větší a hlavně PROČ?

1.2.3.4.5...1004 a 1004^502

(tečka znamená krát a ^znamená mocnina)

Hm? :-)

lukaszh · 04. 04. 2008 16:52

Vyzera to tak, ze faktorial je vacsi. Ked mas f(x)=x! je to rychlejsie rastuca funkcia ako g(x)=x^n.

Olin · 04. 04. 2008 17:00 — Editoval Olin (04. 04. 2008 17:01)

↑ lukaszh:
Jenže teprv až od určité meze, která je pokud vím zhruba n.

Saturday · 04. 04. 2008 17:34

@mp3jj: Pro libovolné n platí nerovnost: 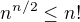$n^{n/2}\le n!$ , důkaz věty můžeš najít v knize Matouška a Nešetřila: Kapitoly z diskrétní matematiky (na tomto fóru jsem již dával odkaz s touto knihou) [pokud si chceš důkaz zkusit sám, tak se zaměř na AG-nerovnost]

mp3jj · 05. 04. 2008 14:48

Saturday napsal(a):
@mp3jj: Pro libovolné n platí nerovnost: $n^{n/2}\le n!$ , důkaz věty můžeš najít v knize Matouška a Nešetřila: Kapitoly z diskrétní matematiky (na tomto fóru jsem již dával odkaz s touto knihou) [pokud si chceš důkaz zkusit sám, tak se zaměř na AG-nerovnost]

Promiň, nemůžu najít ten odkaz :( napiš mi ho prosím...(pokud bys byl tak hodný tak odkaz přesně na důkaz té věty . dííkyyY!!!!! :-) )

Saturday · 05. 04. 2008 15:02

http://mff.cz/data/kapitoly.zip - kapitola odhady faktorialu, najdes to rychle..

liquid · 11. 04. 2008 15:51

porovnej
70! + 73!
a
71! + 72!

jak na to prosim :) ?

jelena · 11. 04. 2008 15:56

↑ liquid:

Rozloz na soucin smerem ke stejnemu "nejmensimu" faktorialu - tady k 70! a vytkni treba 72! = 72*71*70!

OK?

liquid · 11. 04. 2008 16:34

jasne, diky !

Matematické Fórum

#1 04. 04. 2008 16:36

n!, x^n

#2 04. 04. 2008 16:52

Re: n!, x^n

#3 04. 04. 2008 17:00 — Editoval Olin (04. 04. 2008 17:01)

Re: n!, x^n

#4 04. 04. 2008 17:34

Re: n!, x^n

#5 05. 04. 2008 14:48

Re: n!, x^n

Saturday napsal(a):

#6 05. 04. 2008 15:02

Re: n!, x^n

#7 11. 04. 2008 15:51

Re: n!, x^n

#8 11. 04. 2008 15:56

Re: n!, x^n

#9 11. 04. 2008 16:34

Re: n!, x^n

Zápatí