Matematické Fórum

Frantik88

Ahoj všichni,
řeším momentálně příklad, zadání viz. níže, a rád bych se zeptal, zdali můj postup řešení je správný či ne.

Zadání:
Mějme množiny X={1,2,3,4,5} a Y={3,4}. Na potenční množině P(X) definujeme relaci R takto:

$aRb \Leftrightarrow a \cup Y = b \cup Y$ $a,b \in P(X)$

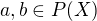
Ukažte, že R je ekvivalence na P(X).

Řešení:

Aby relace byla ekvivalence, musí mít vlastnosti: reflexivita, symetrie a tranzitivita.

Reflexivita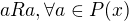
$aRa, \forall a \in P(x)$ , tedy musí platit, že 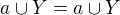$a \cup Y = a \cup Y$ , to platí vždy.

Symetrie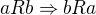
$aRb \Rightarrow bRa$ , tedy musí platit, že 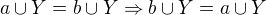$a \cup Y = b \cup Y \Rightarrow b \cup Y = a \cup Y$ , to taky platí vždy.

Tranzitivita: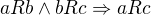

$aRb \wedge bRc \Rightarrow aRc$ , tedy musí platit, že 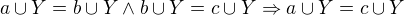$a \cup Y = b \cup Y \wedge b \cup Y = c \cup Y \Rightarrow a \cup Y = c \cup Y$ , to taky platí vždy.

Toto je mé řešení, je třeba to nějakým způsobem rozvádět? Či to, co jsem napsal je dostatečný důkaz?

Děkuji :-)

mikee · 09. 11. 2010 23:38

↑ Frantik88:
Myslim, ze to je dostatocny a spravny dokaz :)

Matematické Fórum

#1 08. 11. 2010 14:36 — Editoval Frantik88 (08. 11. 2010 14:37)

Ekvivalence

#2 09. 11. 2010 23:38

Re: Ekvivalence

Zápatí