Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 11. 2010 21:06
Teorie grafů - zadání č.7
Dobrý den, prosil bych o objasnění zadání projektu 7:
Teorie grafů
K-land je ostrovní země se silniční sítí, která má konečný počet křižovatek a na každé z nich se kříží přesně K cest (O K je známo pouze to, že je více než sedmnáct.). Ukažte, že můžete vyjít z nějaké křižovatky, projít alespoň K+1 různých cest, alespoň K+1 různých křižovatek, a až pak se vrátit na výchozí křižovatku.
Poznámka: Mimoúrovňová křížení cest jsou povolena, v těchto případech se nejedná o křižovatky!
Pokud nejsou pojmy "silniční síť", "křižovatka" nějak definované (např. cesta v teorii grafů má nějaký význam), pak zadání tratí smysl.
Např: Na ostrově existuje silniční síť ve tvaru osmičky a tím jedna křižovatka (není mimoúrovňové), takže z křižovatky vycházejí 4 cesty/vývody ... nevím, jestli by byly podle zadání myšleny jako 1, 2 nebo 4 cesty. Vezmu, že jde o 4 cesty, pak podle zadání se na jedné křižovatce kříží K>17 cest, takže přidám např další 4 osmičky tak, že se jejich "středy" budou křížit na jednom místě ... tím dostanu silniční síť s jednou křižovatkou se 20 vývody/cestami - podle zadání by to snad mělo být ok ... jenže pak není co dokazovat.
Díky za objasnění.
Offline
#4 27. 11. 2010 00:31
Re: Teorie grafů - zadání č.7
Žeby se vám nepodařilo najív v grafu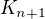 
cyklus délky 
?
Vždyť snadno projdete n+1 různých vrcholů a různých cesta abyste se až v posledním kroku (pak a ne dříve)) vrátil do původního vrcholu.
Offline
#5 27. 11. 2010 20:48
Re: Teorie grafů - zadání č.7
Ukažte, že můžete vyjít z nějaké křižovatky (to je 1 vrchol grafu), projít alespoň K plus 1 různých cest, alespoň K plus 1 různých křižovatek (to je dalsich k plus 1 vrcholov), a až pak se vrátit na výchozí křižovatku (co je ten povodny).
Co znamena, ze mame vyjst z krizovatky, prejst DALSICH k + 1 krizovatiek, roznych, a potom sa vratit do tej povodnej. To znamena, ze by v tom grafe malo byt k + 2 roznych krizovatiek, lebo ta povodna, a este k + 1 inych. A v grafe K_{k + 1} je len k + 1 vrcholov.
Ak sa to mysli k + 1 krizovatiek aj vratane tej povodnej, tak potom ano, to sa da... Ja len ak sa mysli k + 1 krizovatiek este okrem tej zadanej, tak sa to podla mna neda. Lebo splna ten graf predpoklady vety, a nesplna tvrdenie, ako som spominal (kedze v K(k + 1) je len k + 1 vrcholov, nie k + 2.
Offline