Matematické Fórum

xificurC

Predpokladajme, ze ludsky kapital je jedinym vstupom do produkcie a ze funkcia f je striktne rastuca, konkavna a spojite diferencovatelna, pricom $f(0)=0$ , $\lim_{L \to 0}f'(L)=\infty$ , $\lim_{L \to \infty}f'(L)=0$ . Nech U predstavuje preferencie zakaznika. Predpokladajme, ze U je striktne rastuca, konkavna a spojite diferencovatelna, pricom $\lim_{c \to 0}U'(c)=\infty$ , $\lim_{c \to \infty}U'(c)=0$ . Potom problem optimalneho rastu mozno zapisat ako
$\max_{\{ k_{t+1}\}_{t=0}^\infty } \sum_{t=0}^\infty \beta^t U(f[k_t \phi (k_{t+1}/k_t)])$
$(1-\delta)k_t \leq k_{t+1} \leq (1+\lambda ) k_t$
$k_0 > 0$ dane
$\phi(k_{t+1}/k_t)$ je striktne klesajúca, konkávna a spojite diferencovatelna
Asociavana funkcionalna rovnica ma potom tvar
$v(k) = \max_{(1-\delta)k \leq y \leq (1+\lambda )k} \{ U(f[k\phi (y/k)]) + \beta v(y)}$

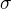Uloha: Nech $F(L)=L^\alpha$ kde $0 < \alpha < 1$ a $U(c)=\frac{c^\sigma}{\sigma}$ kde $\sigma < 1$ . Ukazte, ze v takomto pripade ma funkcionalna rovnica tvar $v(k) = A k^{\alpha \sigma}$ , kde A (citujem) "has the same sign as $\sigma$ ". Ukazte, ze optimalnou strategiou je konstantna miera rastu pre ludsky kapital: $g(k)=\theta k$ pre niektore $\theta > 0$ .

Rad by som poslal nejake napady/zaciatok riesenia, ale zatial do toho vobec nevidim. Skusil som dosadit tie funckie do rovnice v(k), pricom som predpokladal, ze maximum dosiahneme pre y=(1+lambda)k a vypadlo nieco taketo: $v(k) = \frac{k^{\alpha \sigma} {\phi (1+\sigma)}^{\alpha \sigma}}{\sigma}+\beta v((1+\lambda)k)$ .

Za kazdu pomoc budem velmi vdacny.

lukaszh · 24. 11. 2010 18:51

↑ xificurC:

To je ale hnus! Otrasné zadanie. Teraz sa nerozplývam nad tebou, ale nad človekom, ktorý dokáže (praktický??) problém takto sformulovať. Zaradil by som ho do TOP3. Dosť ale osobných výlevov.

Možno neporadím, ale zaujímalo by ma, čo je $\phi$ ? V predpokladoch o nej nepadlo ani slovo. Predpokladám, že U je úžitková funkcia. Treba ukázať, že $v(k)=Ak^{\alpha\sigma}$ . Nenapadá ma nič iné ako

$v(k) = \frac{k^{\alpha \sigma} {\phi (1+\sigma)}^{\alpha \sigma}}{\sigma}+\beta v((1+\lambda)k)=\underbrace{\left[\frac{\phi (1+\sigma)^{\alpha \sigma}}{\sigma}+\frac{\beta}{k^{\alpha \sigma}} v((1+\lambda)k)\right]}_{A}\cdot k^{\alpha \sigma}$

Tiež sa tam vyskytuje niečo ako g vo výsledku, neviem čo to je. No snáď poradí niekto. Neviem, absolútne sa v tom nevyznám.

xificurC

Hej no, nechci vidiet tu knihu :)

$\phi(k_{t+1}/k_t)$ je akasi funkcia predstavujuca pracovny cas. Presnejsie nevysvetlim, ale ako som napisal aj vyssie, je to strikne klesaujca, konkavna a spojite diferencovatelna funkcia.

Tvoj napad bol aj jedinym mojim napadom, mensi problem vidim este v tom, ze tam je ta rekurzia, co by ale teoreticky zmenilo len A, pre ktore zadanie nema ziadne ohranicenia, nez to, co som pisal (a pravdu povediac, neviem, co anglicky "has the same sign as" v preklade matematicky znamena).

Funkcia g predstavuje akusi mieru rastu. Jedine, co som este v knihe nasiel, bolo, ze $k_{t+1}=g(k_t)$ pre t=0,1,2,... Zadanie by potom bolo mozne prepisat na nasledovne:
Ukazte, ze optimalnou strategiou je konstantna miera rastu pre ludsky kapital: $k_{t+1}=g(k_t)=\theta k_t$ pre niektore $\theta > 0$ .

Dakujem, ze si aspon skusil poradit, cenim si to ;) Pravdou je, ze som este nestretol nikoho, kto by sa v tom vyznal :)

lukaszh · 24. 11. 2010 19:56

↑ xificurC:

Aha, nevšimol som si popis k $\phi$ .

has the same sign as: má rovnaké znamienko. To znamená, že ak je sigma kladná, tak aj A je kladné. A podobne naopak. Treba to odskúšať. Nech je sigma kladné číslo, teda $\sigma\in(0,1)$ .

Namiesto $\phi(1+\sigma)$ má byť $\phi(1+\lambda)$ ak som nespravil chybu :-)

$A=\frac{\phi (1+\lambda)^{\alpha \sigma}}{\sigma}+\frac{\beta}{k^{\alpha \sigma}} v[(1+\lambda)k]$

O tom znamienku teda toho veľa nevieme, pretože to dosť závisí od $\phi$ . Možno sa to dá nejako obísť. Iná vec je, či skutočne tebou uvedené
je maximum. Funkcia U je síce striktne rastúca a teda sa nadobúda maximum v pravom koncovom bode intervalu, teda v (1+lambda)k, ale o v(y) nevieme nič. Len to, že vyhovuje uvedenej rovnici. Ak k tomu máš nejakú teóriu, možno podľa toho, alebo neviem jako inak.

Možno jelena dodá materiál :-)

xificurC · 24. 11. 2010 20:32

↑ lukaszh:

Hej, vdaka za opravu, ma tam byt 1+lambda. No ono to $\phi$ je funkcia predstavujuca iste mnozstvo pracovnej doby, ak som to z teorie spravne pochopil, co by znamenalo, ze je kladne. Znamienka by potom sedeli.

Ten napad s maximom bol este predtym, nez som sa docital, ze $\phi$ je klesajuca funkcia :) Potom uz maximum asi len tak zbrucha neuhadneme. Az tak by to mozno ale ani nevadilo, kedze nehladame presny vysledok, nase pochybnosti mozeme skryt v A-cku :) Proste nech nadobuda maximum v nejakom $y=\xi k$ pricom $\xi$ patri do prislusneho intervalu a vysledne A zapiseme pomocou toho. Co ma este ale trapi je to, ze to $v$ vystupuje aj v tom A-cku. A trapi ma aj druha cast zadania, o ktorej nemam ani paru :(

Matematické Fórum

#1 24. 11. 2010 13:47 — Editoval xificurC (24. 11. 2010 13:58)

Optimalny rast s ludskym kapitalom (aplikovana funkcionalna analyza)

#2 24. 11. 2010 18:51

Re: Optimalny rast s ludskym kapitalom (aplikovana funkcionalna analyza)

#3 24. 11. 2010 19:35 — Editoval xificurC (24. 11. 2010 19:35)

Re: Optimalny rast s ludskym kapitalom (aplikovana funkcionalna analyza)

#4 24. 11. 2010 19:56

Re: Optimalny rast s ludskym kapitalom (aplikovana funkcionalna analyza)

#5 24. 11. 2010 20:32

Re: Optimalny rast s ludskym kapitalom (aplikovana funkcionalna analyza)

Zápatí