Matematické Fórum

Ivana · 09. 04. 2008 19:38

Zdravím Vás všechny , kdo máte rádi zajímavé úlohy . S touhle si zatím nevím rady . Mohl by mi někdo pomoci ? Děkuji . :-)

Číslo 3025 jsem roztrhla na 30 a 25 . Když je sečtu a umocním dostanu původní číslo 3025 .
Najdi další čtyřciferné číslo , které má všechny číslice navzájem různé a po rozdělení uprostřed se budou chovat stejně .

halogan · 09. 04. 2008 20:15

$(x + y)^2 = x*100 + y \nl x^2 + x(2y - 100) + y^2 - y = 0$
Dál jsem se nedostal :) Po dosazení x člověk dostane kvadratickou rovnici s y. Otázka je, kdy vyjde celé y. Mně vyšlo třeba u dvacítky.

Saturday

Tak já vykopnu...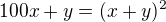

$100x + y = (x+y)^2$

dosadím y = 25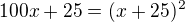

$100x + 25 = (x+25)^2$
$100x + 25 = x^2 + 50x + 625$
$0 = x^2 - 50x + 600$

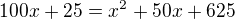
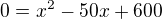
a tato kvadraticka rovnice ma dve reseni: x1 = 20 a x2 = 30

vysledne cislo je tedy 2025

dosazenim x se nic neziska, koren druhy koren je zaporny..

Obecne reseni vsak neznam, toto je spise trik.. :-)

halogan · 09. 04. 2008 21:04

↑ Saturday:

Vykopnes? Chces rict prezentujes stejne reseni a zopakujes muj vysledek? :)) Musel sem si rejpnout :P

Saturday

↑ halogan: vyselo mi to na monitoru nejakou dobu, tvuj prispevek jsem necetl..

nicmene, pokud se podivas do zadani, tak obe reseni jsou ekvivaletne spatne ;)

Olin · 09. 04. 2008 21:16

Diskriminant rovnice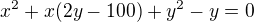
$x^2 + x(2y - 100) + y^2 - y = 0$
je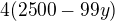
$4(2500-99y)$
s čímž už se dá pracovat ;) Např. úvaha pro která y je toto druhou mocninou celého čísla…

Ivana · 09. 04. 2008 21:19

↑ Saturday:Tam se nesmí číslice opakovat , proto 2025 nelze . Dvojka je tam dvakrát . :-(

Saturday · 09. 04. 2008 21:20

↑ Ivana: Ano, psal jsem to o dva prispevky vyse ;-), nuze pole je porad otevrene :)

Olin · 09. 04. 2008 21:25

Mám řešení brutální silou (vyzkoušení všech dvojic od [1, 1] po [99, 99] strojem), takže znám správný výsledek… Ale prozrazovat ho zatím nebudu, nebo mám?

Ivana · 09. 04. 2008 21:27

↑ Olin:Zdravím , zatím ne . :-)

Alesak · 09. 04. 2008 21:57 — Editoval Alesak (09. 04. 2008 22:03)

mam napad, ale trochu matematicky slozitej. ta rovnice co psal halogan je natocena parabola(zjistil sem to na graficky kalkulacce) cca o -120 stupnu. kdyz by to nekdo dokazal natocit zpatky na tvar y = a*x^2 + b*x +c, tak bysme meli obycejnou parabolu. ta se protina s osou x v bodech 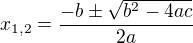$x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$ . ted x musi bejt prirozeny cislo, to znamena ze musi platit rovnice s parametrem $-b\pm\sqrt{b^2-4ac} = k2a$ , kde za k je prirozenej parametr {1, 2, 3...} a koeficienty a a b zname, takze c bude promena, a hodnota y(ted me ale napadlo, ze y nemusi bejt prirozeny?). z ty muzeme dosazenim zjistit x.

vazne si tim nejsem jistej, a vubec netusim jak cokoliv natocit. mozna to de zdravim selskym, ale nic me nenapada

edit: jeste me napadlo ze takle bysme dostali prirozeny cisla jenom pro tu parabolu y =..., a zase bysme to museli natocit zpatky, coz uz by nemuseli bejt prirozeny cisla. takze asi nic.

Ivana · 09. 04. 2008 22:01

↑ Olin:Než odejdeš z fora , a nebudeme-li mít řešení mohl bys ho poslat ? Děkuji . :-)

Olin · 09. 04. 2008 22:02 — Editoval Olin (09. 04. 2008 22:03)

Já vidím jako klíčové řešit, kdy je diskriminant druhá mocnina, tedy platí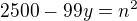
$2500 - 99y = n^2$

Těžko říct, jestli je jednodušší (rychlejší) postupně dosazovat, nebo si vyřešit kongruenci
$n^2 \equiv 2500 (\mathrm{mod }99)\nl n^2 \equiv 25 (\mathrm{mod }99)$

Ivana: Takže to mám hned teď poslat? Už tu dlouho nebudu…

Ivana · 09. 04. 2008 22:12

↑ Olin:Prosím , pošli . :-)Díky .

Olin · 09. 04. 2008 22:16

9801

Ivana · 09. 04. 2008 22:18

↑ Olin:Ano je vychází to :-)

Olin · 09. 04. 2008 22:20

↑ Ivana: Už jsem snad i přišel na poněkud matematičtější postup, řešení té kongruence se totiž dá převést na
$99|(n+5)(n-5)$
což už pak jde.

Matematické Fórum

#1 09. 04. 2008 19:38

Úloha s číslicemi

#2 09. 04. 2008 20:15

Re: Úloha s číslicemi

#3 09. 04. 2008 20:59 — Editoval Saturday (09. 04. 2008 21:02)

Re: Úloha s číslicemi

#4 09. 04. 2008 21:04

Re: Úloha s číslicemi

#5 09. 04. 2008 21:07 — Editoval Saturday (09. 04. 2008 21:11)

Re: Úloha s číslicemi

#6 09. 04. 2008 21:16

Re: Úloha s číslicemi

#7 09. 04. 2008 21:19

Re: Úloha s číslicemi

#8 09. 04. 2008 21:20

Re: Úloha s číslicemi

#9 09. 04. 2008 21:25

Re: Úloha s číslicemi

#10 09. 04. 2008 21:27

Re: Úloha s číslicemi

#11 09. 04. 2008 21:57 — Editoval Alesak (09. 04. 2008 22:03)

Re: Úloha s číslicemi

#12 09. 04. 2008 22:01

Re: Úloha s číslicemi

#13 09. 04. 2008 22:02 — Editoval Olin (09. 04. 2008 22:03)

Re: Úloha s číslicemi

#14 09. 04. 2008 22:12

Re: Úloha s číslicemi

#15 09. 04. 2008 22:16

Re: Úloha s číslicemi

#16 09. 04. 2008 22:18

Re: Úloha s číslicemi

#17 09. 04. 2008 22:20

Re: Úloha s číslicemi

Zápatí