Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 12. 2010 20:17
Pravidelný n-úhelník
Dobrý večer na foru :-)
prosím o pomoc s tímto příkladem :
Kolik vrcholů má pravidelný n-úhelník, jehož všechny vnitřní úhly mají velikost 144° .
Výsledkem je n=10 . Předpokládám tedy, že jde o pravidelný desetiúhelník.
1. Je na výpočet vrcholů v n-úhelníku nějaký vzorec ? Nenašla jsem jej.
2. Souvisí snad 144° se středovým úhlem 72°, který platí pro pětiúhelník ?
Za odpovědi děkuji :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
- (téma jako vyřešené označil(a) Ivana)
#2 15. 12. 2010 20:31 — Editoval BakyX (15. 12. 2010 20:33)
Re: Pravidelný n-úhelník
Čau
1. Je. Súčet všetkých vnútorných uhlov pravidelného n-uholníka je 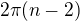 . Z toho si odvodíš "uhol pri vrchole", tak, že delíš "n".
. Z toho si odvodíš "uhol pri vrchole", tak, že delíš "n".
2. Na základe vzorca si to môžeš odovôdniť.
1^6 - 2^6 + 3^6 = 666
Offline
#3 15. 12. 2010 20:43 — Editoval Ivana (15. 12. 2010 20:47)
Re: Pravidelný n-úhelník
↑ BakyX: Moc tomu nerozumím :-(
Těch 144° je jeden vnitřní úhel a pokud jde o desetiúhelník, na což se v úloze ptají, pak výsledný součet všech vnitřních úhlů je 1440°.  .. z toho mu nevychází , že
.. z toho mu nevychází , že 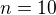
Tak už to mám : 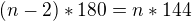 ...
... 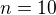
↑ BakyX:... čau a děkuji za pomoc :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline