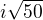Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2008 21:27 — Editoval cecha (16. 04. 2008 21:30)
záporný diskriminant
Dobrý den , chodím do 9. třídy ale dost mě zajímá matematika tak tu a tam zkouším počítat těžší věci no a zkoušel jsem kvadratickou rovnici .. pokud mi vyjde diskriminant kladný tak je to v pohodě a oba kořeny vypočítám ale když vyjde záporný tak nevím jak odmocnit záporný diskriminant .. brácha mi to sice kdysi vysvětloval ale moc jsem to nepochopil tak kdyby byl někdo tak hodný byl bych mu moc vděčný ... jinak kořeny počítám ze vzorce  no akdyž tam je záporný diskriminant tak je vzorec nějak
no akdyž tam je záporný diskriminant tak je vzorec nějak 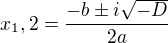 pls nekdo mi to vysvětlete
pls nekdo mi to vysvětlete
Offline
#3 16. 04. 2008 21:36
#5 17. 04. 2008 09:20 — Editoval Ginco (17. 04. 2008 09:22)
Re: záporný diskriminant
↑ Alesak:
Rovnice v C, souhlasim, ale nerovnice jdou řešit v R
je vidět, že se to dá řešit jen v C, ale když doplníme na čtverec, tak dostaneme 
ted už vím, že výraz 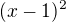 bude vždy kladný, a pokud ke kladnému výrazu přičtu +4, tak je levá strana nerovnice vždy kladná, tedy
bude vždy kladný, a pokud ke kladnému výrazu přičtu +4, tak je levá strana nerovnice vždy kladná, tedy 
ale někdy to nejde, třeba u rovnic se to puožít nedá, nebo? akorát vyjde, že v R nemá řešení.
Tedy musím řešit přes komplexní čísla
Offline

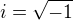 . pak kdyz mas treba
. pak kdyz mas treba 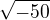 , tak to je
, tak to je 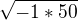 ,
, 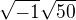 a to je
a to je