Matematické Fórum

Hlavny rozdiel medzi variaciami a kombinaciami je, ze pri variaciach zalezi na poradi, pricom pri kombinaciach nie. Permutacie su specialnym pripadom variacii.
Teda ked budeme rozpravat o pocte moznosti vytvorenia 4-ciferneho cisla _ _ _ _ z cislic {1,2,3,4} , podme premyslat. Zalezi na poradi cislic? Urcite ano, teda budu to variacie. Kolko mame moznosti? Na prve miesto mozme dosadit lubovolnu cislicu, teda moznosti je [4] _ _ _ . Dalej, ci sa cisla mozu alebo nemozu opakovat. Ak sa mozu, pocet moznosti bude logicky [4] [4] [4] [4] , teda 4^4 (pocet cislic (mnoziny) na pocet miest, n^k). Ak sa opakovat nemozu, vysledkom bude [4] [3] [2] [1] , teda 4! , co je v tomto pripade prave pocet permutacii bez opakovania. Ked je pocet cislic a miest rovny (n=k), hovorime o permutaciach a vysledkom je jednoducho n!. Kebyze mame na vyber cislice {1,2,3,4,5,6} , vidime, ze celu mnozinu neminieme. Vysledkom bude [6] [5] [4] [3] , teda vztah pre variacie bez opakovania nam vyjde n! / (n-k)!  Odtial aj vidno, ako nam vyjde vztah pre permutacie, kedy n=k.
No a co s kombinaciami? Zoberme podobny priklad, chceme zistit, kolko stvorclennych skupin mozme vytvorit zo siestich ludi. Mnozinou n teda nadalej bude {1,2,3,4,5,6} a k je znovu rovne styrom, lenze tentoraz na poradi zalezat nebude. Skupina 1,2,4,5 je rovnaka ako skupina 5,2,4,1 , pricom pri variacii cisla 1245 a 5241 su rozne. Nuz, vzorec by som odvodil asi nasledovne: zoberme si vysledok z variacii tohto prikladu a podme ho skumat. Vysledkom je n! / (n-k)! . Toto cislo je jednoznacne vacsie, ako pocet kombinacii. Otazkou je, kolkokrat je nase riesenie zapocitane do vysledku. Pozrime sa napr. na riesenie 1,2,3,4 . Tato skupina (ako aj kazda ina) sa v rieseni nachadza viacnasobne, s inym poradim clenov, presnejsie s kazdym moznym poradim. Kolko je takychto poradi? No pocet permutacii, teda k!. My vsak chceme, aby tato skupina bola v pocte riesenie len raz, teda cely vysledok predelime tymto cylom. Ked vysledok variacii tohto prikladu predelime poctom permutacii pre k, mal by nam vyjst nas zelany vysledok. Ten teda je n! / (k! * (n-k)!) . A mame vysledok :)

Este k variaciam by som podotkol, ze sa v prikladoch s cislami casto v mnozine vyskytuje aj cislo 0. Vtedy treba dbat na to, aby sa 0 na prve miesto nedostala. Pocitanie bude obdobne, napr. zoberme prvy priklad na stvorclenne cisla a mozinu {0,1,2,3} a zratajme variacie s aj bez opakovania. Na prve miesto mozme dosadit len tri cisla, teda dalej budeme hladat len variacie pre trojcislie. Pri opakovani vyjde 3 * V'(3,4) /variacie s opakovanim tretej triedy zo styroch prvkov, V(k,n)/ = 3 * 4^3 .  A ked bez opakovania, tak 3 * P(3) /permutacie tretej triedy (nulu sme uz vyuzili)/ = 3 * 3!  . A podobne sa riesia priklady, ked chcu, aby cislo bolo parne/neparne, delitelne piatimi...

Nejasnosti, chyby, atd, vsetko sem na mna vrhajte :)

↑ vogel: No a jedna poznamka z druhej strany - ak vasa dcera dostane ulohu kombinatorickeho charakteru, je ovela uzitocnejsie ako zistovat, ci ide o take alebo onake variacie, kombinacie, ci permutacie, snazit sa ju vyriesit normalnym uvazovanim. V 95 percentach to ide a je to ovela spolahlivejsi sposob. Obvykle staci pamatat si dve veci:

1. ak chceme zoradit do radu ludi, da sa to urobit sposobmi.

2. ak je muzov a zien, tak mozu vytvorit 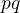roznych tanecnych parov.

S tymito skutocnostami sa jej podari vyriesit takmer vsetky skolske ulohy. A samozrejme s pouzitim zdraveho rozumu.