Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 01. 2011 18:09 — Editoval Lancer (10. 01. 2011 18:14)
Exponencialna rovnica
Najdite vsetky riesenia rovnice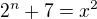 
v celych cislach.
-
Najprv ma napadlo, ze na pravej strane je neparne cislo, teda 
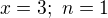musi byt neparnym cislom tiez. Nasiel som tak 2 riesenia 
a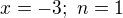 
. A ked som si dal pocitacom vykreslit graf funkcie, zistil som, ze ziadne dalsie uz neexistuju. Ako to vsak mam dokazat? Dakujem za pomoc. Slovencina dufam nevadi.
Offline
#2 10. 01. 2011 18:32 — Editoval Alan122 (10. 01. 2011 18:33)
Re: Exponencialna rovnica
↑ Lancer:
skusim po odčítaní 7 máme že lavá strana je delitelná 2 potom aj pravá čiže x^2 je kongruentné so 7 mod 2 čiže x^2 je kongruentné s 1 mod 2 teda x=2k+1 pre nejaké celé k. Dosadíme a máme 2^n=4k^2+4k-6
pričítame 2 máme 2^n + 2= 4k^2+4k-4
2(2^n-1 +1)= 4(k^2 +k -1)
2^n-1 +1= 2(k^2 +k -1) pravá je delitelná 2 musi aj lava a to je iba pre n=1
x dopočítaš
Offline
#3 10. 01. 2011 18:35
Offline