Matematické Fórum

Krezz · 11. 01. 2011 22:47

Ahoj, mam takovej problem s rovnici.
$y''+4y=0$
Podmínky
$y(0)=2 ; y'(0)=3$
Rozklad na lambdy chapu. Nechapu ale kdyz dostani v tomto pripade 2i a -2i jak z toho udelam fce sinus cosinus do obecneho reseni. To ma byt asi takto:
$y(x)=c1.cos2x+c2.sin2x$

Pavel Brožek

Jde pouze o volbu báze prostoru řešení. Jedna báze prostoru řešení je 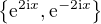$\{\mathrm{e}^{2\mathrm{i}x},\mathrm{e}^{-2\mathrm{i}x}\}$ (předpokládám, že v té řešení umíš vyjádřit), druhá 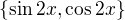$\{\sin2x,\cos2x\}$ . Přechod mezi těmito bázemi je dán vztahy

$\sin2x=\frac{\mathrm{e}^{2\mathrm{i}x}-\mathrm{e}^{-2\mathrm{i}x}}{2\mathrm{i}}\nl \cos2x=\frac{\mathrm{e}^{2\mathrm{i}x}+\mathrm{e}^{-2\mathrm{i}x}}{2}$

(Vychází to ze známých vzorců pro sinus a kosinus.)

Krezz · 11. 01. 2011 23:24

jelikož mám zitra zkousku tak se tim nechci zatezovat, ale jestli tomu rozumim spravne tak ten prevod ikdyz je ve vysledcich neni nutny? Muzu klidne postupovat podle toho obecneho vzorce e^lamdax?

Me jde o to, ze pokud vyjadrim obecne reseni podle toho jak to umim, tak me vyjde: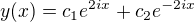
$y(x)=c_1e^{2ix}+c_2e^{-2ix}$
a v knize je
$y(x)=c_1cos2x+c_2sin2x$
to by potom znamenalo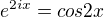
$e^{2ix}=cos2x$
což bude nejspis blbost :D

Pavel Brožek

↑ Krezz:

Tvůj výsledek a výsledek z knihy jsou oba správně. V žádném případě to však neznamená 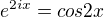$e^{2ix}=cos2x$ . Znamená to pouze to, že všechny funkce, které se dají vyjádřit ve tvaru

$c_1e^{2ix}+c_2e^{-2ix}\qquad c_1,c_2\in\mathbb{C}$

se dají vyjádřit i ve tvaru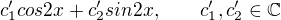

$c_1'cos2x+c_2'sin2x,\qquad c_1',c_2'\in\mathbb{C}$

a naopak.

Pro jednu danou funkci ale nebudou nečárkované a čárkované konstanty stejné.

Ještě jinak řečeno: Do lineární obalu funkcí 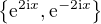$\{\mathrm{e}^{2\mathrm{i}x},\mathrm{e}^{-2\mathrm{i}x}\}$ a do lineárního obalu funkcí 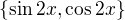$\{\sin2x,\cos2x\}$ patří ty samé funkce. Ale jejich souřadnice vzhledem k různým bázím (souřadnice jsou ty nečárkované a čárkované konstanty) budou obecně různé.

Edit: Ta báze z knihy se ale často upřednostňuje, má to své dobré důvody, např. proto, že jde o reálné funkce.

Krezz · 12. 01. 2011 00:00

Jasny chapu, ale stejne mi to neda, kdybych chtel uzit te druhe verze s goniometrickymi funkcemi, jak bych takovy priklad resil? Ten vztah co si mi napsal uplne nahore totiz vubec nevim jak pouzit. Vyjdou me lambdy ale jak z nich udelam gon. fce nevim. V knize jsou reseny vsechny priklady obdobne, k testu ani zkousce se to nevyzaduje, ale rad bych to vedel. Rad delam veci poradne. Pravda je ze to vysledne partikularni reseni je urcite prijememnejsi v te druhe verzi nez v te moji.

Pavel Brožek · 12. 01. 2011 00:14

↑ Krezz:

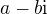Pokud máš diferenciální rovnici pouze s reálnými koeficienty, pak má nutně i charakteristický polynom reálné koeficienty. Z toho plyne, že má pouze reálné kořeny a dvojice komplexně sdružených kořenů. Nechť $a+b\mathrm{i}$ (a, b reálná, b různé od nuly) je jedním takovým komplexním kořenem. Pak i $a-b\mathrm{i}$ je kořenem. Rovnici tedy bude řešit (mimo další řešení) dvojice funkcí $\{\mathrm{e}^{(a+b\mathrm{i})x},\mathrm{e}^{(a-b\mathrm{i})x}\}$ . Můžeme udělat dvě lineární kombinace těchto funkcí:

$\frac12\mathrm{e}^{(a+b\mathrm{i})x}+\frac12\mathrm{e}^{(a-b\mathrm{i})x}=\mathrm{e}^{ax}\cdot\frac{\mathrm{e}^{\mathrm{i}bx}+\mathrm{e}^{-\mathrm{i}bx}}{2}=\mathrm{e}^{ax}\cdot\cos bx\nl \frac1{2\mathrm{i}}\mathrm{e}^{(a+b\mathrm{i})x}-\frac1{2\mathrm{i}}\mathrm{e}^{(a-b\mathrm{i})x}=\mathrm{e}^{ax}\cdot\frac{\mathrm{e}^{\mathrm{i}bx}-\mathrm{e}^{-\mathrm{i}bx}}{2\mathrm{i}}=\mathrm{e}^{ax}\cdot\sin bx$

(V našem případě bylo a=0.)

Tím se dostáváme k nové bázi. Vidíš tedy, že pokud máš reálné koeficienty, tak když ti vyjde komplexní kořen $a+b\mathrm{i}$ , tak v bázi řešení budou funkce $\{\mathrm{e}^{ax}\cdot\cos bx,\mathrm{e}^{ax}\cdot\sin bx\}$ . (My jsme to myslím měli v přednáškách jako větu, která se snadno dokázala, pak už nebylo nutné příliš přemýšlet o nějaké bázi $\{\mathrm{e}^{(a+b\mathrm{i})x},\mathrm{e}^{(a-b\mathrm{i})x}\}$ )

Rumburak

↑ Krezz:
V zásadě jde o to, že obyčejnou lineární dif. rovnici můžeme obecně chápat jako úlohu v komplexním oboru, tj. neznámá funkce je
komplexní funkcí komplexní proměnné, derivace v rovnici jsou derivacemi podle této kompl. proměnné.
Pokud Tě zajímá takto koncipované řešení v komplexním oboru, pak není problém použít jako bázi prostoru řešení dvojici

(1) $\{\mathrm{e}^{(a+b\mathrm{i})x},\,\mathrm{e}^{(a-b\mathrm{i})x}\}$ ,

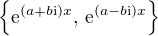jou-li 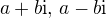$a+b\mathrm{i}, \,a-b\mathrm{i}$ charakteristická čísla příslušné rovnice druhého řádu.

Avšak v mnoha úlohách, i když charakteristická čísla rovnice reálná nejsou (například při vyšetřování harmonického pohybu), nás
přesto zajímají pouze reálná řešení (tj. neznámou funkcí má být reálná funkce reálné proměnné, derivace v rovnici jsou derivacemi
podle této reálné proměnné). V tom případě jako bázi prostoru řešení použijeme dvojici

$\{\mathrm{e}^{ax}\cdot\cos bx,\,\mathrm{e}^{ax}\cdot\sin bx\}$ ,

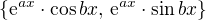která by při "komplexní úloze" s komplexní proměnnou x měla tentýž lineární obal jako báze (1) , avšak při reálné proměnné x z ní
dostaneme pouze reálné funkce, jak potřebujeme.

Matematické Fórum

#1 11. 01. 2011 22:47

Diferencialni rovnice

#2 11. 01. 2011 22:51 — Editoval BrozekP (11. 01. 2011 22:53)

Re: Diferencialni rovnice

#3 11. 01. 2011 23:24

Re: Diferencialni rovnice

#4 11. 01. 2011 23:53 — Editoval BrozekP (12. 01. 2011 00:00)

Re: Diferencialni rovnice

#5 12. 01. 2011 00:00

Re: Diferencialni rovnice

#6 12. 01. 2011 00:14

Re: Diferencialni rovnice

#7 12. 01. 2011 10:06 — Editoval Rumburak (12. 01. 2011 14:34)

Re: Diferencialni rovnice

Zápatí