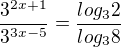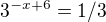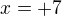Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kombinace exponencialni a logaritmicke rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 04. 2008 18:04
Kombinace exponencialni a logaritmicke rovnice
čau lidičky, potřeboval bych prosím pomoc s tímto příkladem, u kterého mě velice zajimá postup, díky.
3^2x+1 . log(3)8 = 3^3x-5 . log(3)2 v R
základy logaritmů jsou v kulatých závorkách
výsledek : x = 7
Offline
- (téma jako vyřešené označil(a) Dana1)
#4 24. 04. 2008 18:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinace exponencialni a logaritmicke rovnice
↑ liquid:
Zdravim :-) delas mi samou radost, fakt dobre :-) - jen v zadani je 3^3x-5 - dopln, prosim, 3 do mocniny v citateli. Ale to je zcela zanedbatelny detail :-)
Offline
#6 24. 04. 2008 18:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinace exponencialni a logaritmicke rovnice
↑ Vlastik: ale, co ja :-) metodicky a systematicky to zajistil kolega prece :-)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kombinace exponencialni a logaritmicke rovnice (TOTO TÉMA JE VYŘEŠENÉ)