Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Fourierov rad - pomoc surne (TOTO TÉMA JE VYŘEŠENÉ)
#2 15. 01. 2011 21:12
Re: Fourierov rad - pomoc surne
↑ jeree01:
Můžu ti doporučit možná tak tohle: http://www.google.cz/#sclient=psy&h … 2d22e110c8.
Jinak kromě per partes neumíš použít ani Newtonovu formuli pro výpočet určitého integrálu -  musí být dvojnásobek střední hodnoty funkce, a ta je evidentně 1,5. Dosazuješ meze ve špatném pořadí.
musí být dvojnásobek střední hodnoty funkce, a ta je evidentně 1,5. Dosazuješ meze ve špatném pořadí.
Offline
#3 15. 01. 2011 21:55
Re: Fourierov rad - pomoc surne
↑ r_izz_o:
OK,malo byt F(b)-F(a) ....
a co ten per partes? zatial mam ![kopírovat do textarea $[(\frac{x^2}2+x)cos(2\pi nx)]_0^1-\int_0^1-sin(2\pi nx)\frac{x^2}2+x dx$](/mathtex/f3/f3ddae48b6b05e7d9d774e39e7c845f5.gif)
Offline
#4 15. 01. 2011 22:43
Re: Fourierov rad - pomoc surne
↑ jeree01:
Pokud budeš integrovat (x+1) a ten sin/cos derivovat, tak si práci moc nezjednodušíš..
Offline
#5 15. 01. 2011 22:52
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: Fourierov rad - pomoc surne
vysledek se da zkontrolovat na http://cgi.math.muni.cz/~kriz/xsrot/fou … ulator.cgi
Offline
#7 15. 01. 2011 23:54
Re: Fourierov rad - pomoc surne
↑ jeree01:
To už je o něco lepší. Akorát je špatně zintegrovaná ta funkce  . Pokud to přímo nevidíš, tak si ten integrál spočítej substitucí
. Pokud to přímo nevidíš, tak si ten integrál spočítej substitucí  . Kontrola je, že si zkusiš ten výsledek zderivovat - a musí vyjít to s čím jsi začínal.
. Kontrola je, že si zkusiš ten výsledek zderivovat - a musí vyjít to s čím jsi začínal.
Vyskočí opravdu ten integrál se sinem, a ten se spočítá stejnou substitucí. Substituce za  tady nepomůže.
tady nepomůže.
Offline
#10 16. 01. 2011 12:33
Re: Fourierov rad - pomoc surne
Tak som to skusal podla podobneho prikladu tuna na fore: http://forum.matweb.cz/viewtopic.php?pid=104707#p104707
a mi vyslo nieco take zatial:
ako dalej?
Offline
#11 16. 01. 2011 17:57
Re: Fourierov rad - pomoc surne
↑ jeree01:
Teď nemám čas to kontrolovat, takže snad se vyjádří někdo z kolegů. Na první pohled to vypadá přinejmenším divně, protože se mi zdá, že rozvíjíš jinou funkci než je v zadání (v zadání je x+1, ty rozvíjíš x). Navíc periodické prodloužení té funkce x na intervalu (0,1) podle mně stejně nebude lichá funkce, takže bych očekával jinou hodnotu  . Ten výpočet integrálu jsem nekontroloval. Jinak si ale uvědom, že n je přirozené číslo, takže výrazy typu
. Ten výpočet integrálu jsem nekontroloval. Jinak si ale uvědom, že n je přirozené číslo, takže výrazy typu  umíš vyčíslit (teda aspoň doufám).
umíš vyčíslit (teda aspoň doufám).
Offline
#12 16. 01. 2011 20:05 — Editoval jeree01 (16. 01. 2011 21:38)
Re: Fourierov rad - pomoc surne
↑ LukasM:
taaak este raz a od zaciatku mi vyslo toto(zatial pre  :
:

takze za  potom dosadim cislo,hmmm,ale jake fakt som nebol na prednaske a z tych skript to nechapem.Tam je to stale na konci pre
potom dosadim cislo,hmmm,ale jake fakt som nebol na prednaske a z tych skript to nechapem.Tam je to stale na konci pre 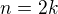 a
a  . Odkial to je?
. Odkial to je?
Alebo nepovedz,ze dosadim 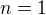 a dostanem
a dostanem 
Ty vole,ono to tak snad aj bude.Vyslo mi toto: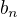


a nakoniec
a uplne nakoniec Fourier trigonometric series calculator hovori:
Takze snad je to dobre.
Offline
#16 17. 01. 2011 20:58
Re: Fourierov rad - pomoc surne
↑ r_izz_o:
jo ,som to tam zabudol pisat,ale vo vysledku  uz je
uz je  dvakrat . Chyby z nepozornosti a zabudanie atd...na to casto doplacam...BTW.Treba tam este nakreslit graf.Viem ako vyzera,ale ako sa k nemu dostanem?
dvakrat . Chyby z nepozornosti a zabudanie atd...na to casto doplacam...BTW.Treba tam este nakreslit graf.Viem ako vyzera,ale ako sa k nemu dostanem?
Offline
#17 17. 01. 2011 21:17
Re: Fourierov rad - pomoc surne
↑ jeree01:↑ jeree01:
pri vysledku An a Bn si vykratil menovatela s dvojkou ..to mozes ked je v menovateli 2pin ale ked je (2pin)^2 tak predsa 2 nemozes skrknut..
Offline
#18 17. 01. 2011 21:22
Re: Fourierov rad - pomoc surne
↑ r_izz_o:
Ja viem....malo tam byt  ,to ked vykratim dvojkou tak bude
,to ked vykratim dvojkou tak bude  ale v konecnom vysledku to bude tak ci tak
ale v konecnom vysledku to bude tak ci tak  ,nie?
,nie?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Fourierov rad - pomoc surne (TOTO TÉMA JE VYŘEŠENÉ)




 potom
potom  ,
,  potom
potom 




 mi vyslo
mi vyslo 
![kopírovat do textarea $[xsin(2\pi nx)+\frac{cos2\pi nx}{2\pi n}+\frac{sin2\pi nx}{2\pi n}]_0^1$](/mathtex/05/054dfcd35690ec74213a7aa7b4ac6a05.gif)



