Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Nerovnost - 16 čísel na kružnici (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 01. 2011 17:24
Nerovnost - 16 čísel na kružnici
Na kružnici máme 16 reálných čísel, jejichž součet je 7.
-Ukažte, že existuje úsek pěti sousedních čísel se součtem alespoň 2.
-Určete nejmenší k takové, že v popsané situaci lze vždy nalézt úsek k sousedních čísel se součtem alespoň 3.
(Letošní úloha školního kola MO-B, které mělo proběhnout v dopoledních hodinách, takže nikomu neuškodí, když tu tento zajímavý příklad bude. Pozn. toto se už odemklo, takže už správci asi nebudou proti...)
+ Něco navíc: určete nejmenší p takové, že v popsané situaci lze vždy nalézt úsek p sousedních čísel se součtem alespoň N.
Moje řešení:
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
- (téma jako vyřešené označil(a) TomDlask)
#2 20. 01. 2011 18:47
Re: Nerovnost - 16 čísel na kružnici
↑ TomDlask:
dnes som tuto ulohu riešil a moje riešenie bolo takmer identicke :D
Offline
#3 20. 01. 2011 19:23
Re: Nerovnost - 16 čísel na kružnici
↑ Alan122: Tak tahle úloha byla jedna z těch jednodušších, jen se musí přijít na ten způsob... Kdo řešil domácí kolo, tak si na to snad vzpomněl.
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#4 20. 01. 2011 19:44
Re: Nerovnost - 16 čísel na kružnici
↑ TomDlask: mně teda nepřijde, že bys tu první část dokázal
Offline
#5 20. 01. 2011 20:10
Re: Nerovnost - 16 čísel na kružnici
↑ Stýv: Neřekl jsem, že mé řešení je správné, kde je tedy v tom postupu chyba?
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#6 20. 01. 2011 20:34
Re: Nerovnost - 16 čísel na kružnici
↑ TomDlask: není tam chyba, jenom to vede jaksi odnikud nikam. to, co píšeš ve skrytym textu, je správně
Offline
#8 01. 02. 2011 15:13
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Nerovnost - 16 čísel na kružnici
Tahle úloha spadá spíš do oboru kombinatoriky. Vím, že tj. maličkost, ale nějak mi to nesedí...
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Nerovnost - 16 čísel na kružnici (TOTO TÉMA JE VYŘEŠENÉ)








 se v nich objeví přesně pětkrát (vystřídá všechny pozice v součtu - první, druhou, třetí, čtvrtou, pátou). Součtem nerovností je tedy tato nerovnost:
se v nich objeví přesně pětkrát (vystřídá všechny pozice v součtu - první, druhou, třetí, čtvrtou, pátou). Součtem nerovností je tedy tato nerovnost:
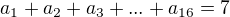 a dostaneme:
a dostaneme:














