Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 01. 2011 09:33 — Editoval Azeret (22. 01. 2011 09:35)
Lingebra - jádro zobrazní
Ahoj,
mám zadaný příklad:
Nechť 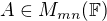 ,
, 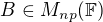 (kde
(kde 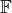 je
je  nebo
nebo  ). Rozhodněte, které z následujících výroků platí a odpověď zdůvodněte:
). Rozhodněte, které z následujících výroků platí a odpověď zdůvodněte:
(a) 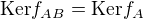
(b) 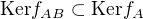
(c) 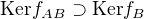
(d) 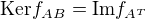
(c) 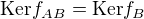
Já myslím, že platí (c) - jádro je množina všech vektorů, které se zobrazí na nulu (tedy homogenní řešení rovnice) - platí 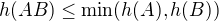 , tedy počet lin závislých řádků bude stejný nebo větší - a proto bude i "větší" jádro.
, tedy počet lin závislých řádků bude stejný nebo větší - a proto bude i "větší" jádro.
A pak už mi přijde, že neplatí nic . . .
Díky za případné rady a kritiky k řešení.
pi = 3
Offline