Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Priklad s parcelami, pravedpodobnost...
#26 25. 01. 2011 15:30
Re: Priklad s parcelami, pravedpodobnost...
↑↑ lacikes:
To prvni je obracene...
Ale spis co to znamena v tomhle konkretnim pripade. Co tady znamena 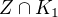 ? Kdyz K1 je losujeme z prvniho klobouku a Z je vylosujeme zlatonosnou parcelu...
? Kdyz K1 je losujeme z prvniho klobouku a Z je vylosujeme zlatonosnou parcelu...
Offline
#27 25. 01. 2011 15:31
Re: Priklad s parcelami, pravedpodobnost...
↑↑ petrkovar:
vlastne je pravdepodobnost Z za predpokladu ze nastal jav K1. tak pravdepodobnost Z=2/7 a pravdepodbnost K1 kedze mame dva klobuky tak by mala byt 1/2, ci sa mylim?
Offline
#28 25. 01. 2011 15:51
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Ano,  je opravdu 1/2.
je opravdu 1/2.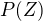 ale není 2/7.
ale není 2/7. 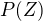 bude řešením celého příkladu, že? (zápis "pravdepodobnost Z=2/7" je opravdu velmi nešťastný)
bude řešením celého příkladu, že? (zápis "pravdepodobnost Z=2/7" je opravdu velmi nešťastný)
Já se však ptal, jaké jsou hodnoty  a
a  ?
?
Offline
#29 25. 01. 2011 16:04
Re: Priklad s parcelami, pravedpodobnost...
↑ petrkovar: = 2/7
= 2/7 = 1/7
= 1/7
to som pocital, ze P(Z) = 2/7 avsak vy vravite, ze to nie su 2/7 tak potom co mam do vzorca dosadit?
Offline
#30 25. 01. 2011 20:35
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Není jasné o jakém vzorci je řeč. Jak jste počítal P(Z)?
Offline
#31 25. 01. 2011 20:42
Re: Priklad s parcelami, pravedpodobnost...
↑ petrkovar:
ja som myslel, ze 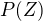 bude pravdepodobnost, ze vytihaneme zlatonosnu parcelu z prveho klobuku, cize 2/7
bude pravdepodobnost, ze vytihaneme zlatonosnu parcelu z prveho klobuku, cize 2/7
Offline
#32 25. 01. 2011 20:50
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Ne, my hledáme odpověď na otázku, zda McGregor získá zlatonosnou parcelu a tento jev onačíme Z (zlato!). Zletonosnou parcelu může získat z prvního i druhého klobouku. Což se musí projevit ve vztahu pro 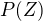 . Jak bude vypadat vztah pro
. Jak bude vypadat vztah pro 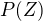 ?
?
Offline
#33 25. 01. 2011 20:54
Re: Priklad s parcelami, pravedpodobnost...
↑ petrkovar:
tak pre prvy klobuk by to mohlo byt (2/7) / 15 ??
Offline
#34 25. 01. 2011 21:08
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Ale kdepak.
Aby nastal jev 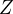 musíme buď vytáhnout zlanonosnou parcelu z prvního klobouku (příslošnou pravděpodobnost už máme vypočítanou výše, která to je a podle jakého vztahu se vypočítala?) a nebo z druhého klobouku. Příslušná druhá pravděpodobnost se vypočítá podobně.
musíme buď vytáhnout zlanonosnou parcelu z prvního klobouku (příslošnou pravděpodobnost už máme vypočítanou výše, která to je a podle jakého vztahu se vypočítala?) a nebo z druhého klobouku. Příslušná druhá pravděpodobnost se vypočítá podobně.
Protože se jedná o dva disjunkntí případy, můžeme pak jednotlivé pravděpodobnosti sečíst.
Offline
#35 25. 01. 2011 21:14
Re: Priklad s parcelami, pravedpodobnost...
↑ petrkovar:
tak pocitali sme tu pravdepodobnost tich 2/7 + 5/8..ale uz som vazne z toho prikladu popleteny cely a neviem co mam pocitat..vsak ked vytahujeme z prveho klobuku mame pravdepodobnost ze vytiahneme zlatonosnu parcelu 2/7, ked vytahujeme z druheho klobuku nastane pravdepodobnost 5/8. Myslel som , ze Z je pre prvy klobuk a nejake potom bude Z2 pre dalsi klobuk a vysledne pravdepodobnosti spocitame.
Offline
#36 25. 01. 2011 21:23
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:
Zde ale opět narážíme na problém, že by prst mohla vyjít > 1. Taky se zamyslete nad výsledkem... očekáváte přeci výsledek někde kolem 50 %, není tak?
Ono sice 2/7 a 5/8 je dobře, ale obojí je podmíněno tím, že si vyberete ten či onen klobouk.
Polopatě
P(vybral sem tenhle klobouk) * P(udělal jsem tuhle akci na základě toho, že jsem si vybral právě tenhle klobouk) + [to samé pro klobouk druhý]
Offline
#37 25. 01. 2011 21:29
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Ano, Vaše argumentace se točí v kruhu.
Všimněte si, že 2/7 je pravděpodobnost, že vytáhneme číslo zlanonosné parcely ZA PŘEDPOKLADU, ŽE TAHÁME Z PRVNÍHO KLOBOUKU. ( )
)
Nás ale zajímá pravděpodobnosti, že z prvního klobouku vytáhneme číslo zlatonosné parcely (tj. SOUČASNE NASTANOU JEVY "taháme z prvního klobouku" a "vytáhneme číslo zlatonosné parcely") 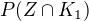 a nebo že z druhého klobouku vytáhneme číslo zlatonosné parcely (detaily doplňte sám).
a nebo že z druhého klobouku vytáhneme číslo zlatonosné parcely (detaily doplňte sám).
Znovu připomínám, že klíčem porozumění je správně pochopení rozdílu  a
a 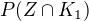 . Ani ne tak symbolům, ale jejich významu.
. Ani ne tak symbolům, ale jejich významu.
Offline
#38 25. 01. 2011 21:36
Re: Priklad s parcelami, pravedpodobnost...
Tento příklad NENÍ jen o dosazování do vzorce. Abychom jej vyřešili, stačí vzít rozum do hrsti. Tolik diskutovaná symbolika nám může pomoci.
... tedy pokud jsme ji během studia dobře ovládli.
Offline
#39 25. 01. 2011 21:52
Re: Priklad s parcelami, pravedpodobnost...
↑ petrkovar: problem asi vidim len v jednom pripade, neviem ako vypocita t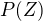 ...
...
Offline
#40 25. 01. 2011 22:09
Re: Priklad s parcelami, pravedpodobnost...
Vždyť už to tu bylo vícekrát psáno. Číslo zlatonosné parcely buď vytáhneme z prvního klobouku nebo z druhého klobouku. To je náš hleadný jev 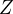 .
.
Pravděpodobnost těchto dvou disjunktních (!) jevů (pečlivě si rozmyslete, proč jsou disjunktní) je součtem jejich pravděpodobností.
Symbolicky zapsáno: 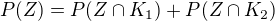
Dosadit není problém. Jak to je s porozuměním?
Offline
#45 26. 01. 2011 10:42
Re: Priklad s parcelami, pravedpodobnost...
↑ lacikes:Výlsedek je správně. Odpovídá doplněnému zadání ve čtvrtém příspěvku a také celé další diskuzi.
Offline
#46 26. 01. 2011 17:36
#47 27. 01. 2011 14:04 — Editoval mysteriouss (27. 01. 2011 14:07)
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Priklad s parcelami, pravedpodobnost...
Jookyn: Zadani bylo vice kazde zadani melo jine hodnoty.
lacikes: ano je jen pozor na zapis ja za ten tvuj zapis "2/7 * 1/2 + 5/8 * 1/2 = 0,455" dostal -5 bodu melo to pry byt: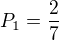
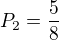
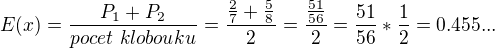
Offline
#48 27. 01. 2011 14:49
Re: Priklad s parcelami, pravedpodobnost...
↑ mysteriouss:Ne, s příspěvkem nesouhlasím.
Zápis 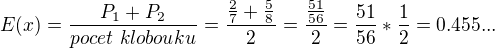 je špatně z několika důvdů. Zejména nepočítáme střední hodnotu. A potom co to je "dělení pravděpodobnosti číslem"?
je špatně z několika důvdů. Zejména nepočítáme střední hodnotu. A potom co to je "dělení pravděpodobnosti číslem"?
Offline
#49 27. 01. 2011 15:28 — Editoval mysteriouss (27. 01. 2011 15:31)
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Priklad s parcelami, pravedpodobnost...
no to deleni cislem 2 je jako ze jelikoz mame 2 klobouky tak je treba to vydelit 2ma kdyby byly 3 tak 3ma, je jedno jestli to cele bude /2 nebo *1/2 ne?
Pokud ne tak jak by to melo prosim byt?
Nic jineho me nenapada.
Offline
#50 27. 01. 2011 15:51
Re: Priklad s parcelami, pravedpodobnost...
↑ mysteriouss:Výpočet je probrán v celém tomto vláknu. Doporučuji si jej prostudovat.
Dělit dvěma pravděpodobnost není korektní postup výpočtu pravděpodobnosti, neboť nemáme žádné tvrzení, podle kterého by takový postup dával správný výsledek.
Že číselně vychází oba výpočty stejně, je svým způsobem náhoda: 1) dvakrát násobit 1/2 a sečíst nebo 2) celý součet vydělit dvěma.
Jak by Váš výpočet vypadal, kdybychom věděli, že jeden klobouk má větší pravděpodobnost, že si jej McGregor vybere, než druhý?
Offline
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Priklad s parcelami, pravedpodobnost...