Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální / logaritmická rce/nerce (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 04. 2008 19:05 — Editoval lopson (29. 04. 2008 19:06)
Exponenciální / logaritmická rce/nerce
Ahoj,
tak jsem počítal dva příklady, ale vůbec si nejsem jist s výsledkem.
Mám určit definiční obor, ale nevím no, myslím, že je špatně. Výsledek neznám.
No a ve druhém:
Mi výsledek hapruje kolem té "dvojky" ona tam patří, protože vyhovuje té absolutní hodnotě???
Jinak se omlouvám za špatnou kvalitu fotek :-×
Diky moc...
Offline
#3 29. 04. 2008 19:21
#6 29. 04. 2008 19:36
Re: Exponenciální / logaritmická rce/nerce
prvni priklad zda se byti v poradku. u druheho prikladu si musis uvedomit, ze resis exponencialni nerovnici, kterou jsi upravil tak, ze staci porovnavat exponenty. dulezite je si ale uvedomit, ze prave zminene dva body -2, 2 jsou svym zpusobem specificke - za prve nuluji absolutni hodnotu a za druhe zpusobi, ze 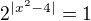 . navrhoval bych tedy vzdy tyto body ve finale primo dosadit do rovnice a overit, zda-li ji splnuji.
. navrhoval bych tedy vzdy tyto body ve finale primo dosadit do rovnice a overit, zda-li ji splnuji.
Offline
#7 29. 04. 2008 20:03 — Editoval lopson (29. 04. 2008 20:04)
Re: Exponenciální / logaritmická rce/nerce
No tak "aritentd" píše, že tam neplatí podmínka ten logaritmus různý od nuly a plisna říká, že je to OK tak nevím no.
A co se týká toho druhého příkladu, tak tam není rovno 1. Nestačilo by tu dvojku pouze dosadit do te abs. hodnoty, vyšlo by, že I0I<2 prohlásili bychom, že je to OK a prostě bychom tam tu dvojku přidali do intervalu?
Offline
#9 29. 04. 2008 20:16
Re: Exponenciální / logaritmická rce/nerce
Tak ja už jsem z toho jelen, jen mi pisněte prosím u toho prvniho příkladu co tam tedy mam dělat udělal jsem tam tedy log(neco) --> "neco" >0 a pak ze se spodek nesmí rovnat nule. Je to špatně, nebo tam ještě něco chybí? Plisna řekl, že je ten def obor správně aritentd zase říká něco jiného.
A u toho druhého příkladu moc nevím, co tím myslíte. Sory
Offline
#11 29. 04. 2008 20:24 — Editoval lopson (29. 04. 2008 20:25)
Re: Exponenciální / logaritmická rce/nerce
Dobře děkuji za ujasnění prvního příkladu.
A teď mi jen prosím řekněte PROČ není důvod je vynechávat ve druhém příkladu. Je to kvůli tomu, že I0I<2, když je tam dosadíme (ty nulové body)? A jestli je to z jiného důvodu prosím o nějaké lajcké vysvětlení? Díky moc.
Offline
#15 29. 04. 2008 20:43 — Editoval lopson (29. 04. 2008 20:47)
Re: Exponenciální / logaritmická rce/nerce
Ojoj, poki, zapřemýšlím....
No napadá mě to snad pomocí tabulky... a v každém intervalu to pak omezit... ? I když asik ne moc daleko bych se asi nedostal. teda nebo pokud je to jen klasická parabola a pak ještě to kvuli abs. hodnotě překlopit přes osu X?
Offline
#17 29. 04. 2008 20:55 — Editoval lopson (29. 04. 2008 21:11)
Re: Exponenciální / logaritmická rce/nerce
No nevím přesně jestli myslím to, co myslíš zrovna ty. Ale moc nevím, co si mám myslet. :-0
Aha jo tak. Uz asik vim. No jsou to takove dva zuby. V bodě +- 2 na ose X?
Rád bych Jeleno znal tvůj názor na postup v tom prvním příkladu? Je správný nebo bys mu něco vytkla?
Jinak, já vím asi jsem moc tvrdohlavý, ale opravdu mi nestačí do té absolutní hodnoty dosadit nulové body, zjistit, že I0I<2 a prohlásit tak, že nulové body vyhovují intervalu?
Offline
#18 29. 04. 2008 21:24 — Editoval aritentd (29. 04. 2008 21:29)
Re: Exponenciální / logaritmická rce/nerce
lopson napsal(a):
Jinak, já vím asi jsem moc tvrdohlavý, ale opravdu mi nestačí do té absolutní hodnoty dosadit nulové body, zjistit, že I0I<2 a prohlásit tak, že nulové body vyhovují intervalu?
urcite to tak jde, alespon v tom nevidim zadny problem. Je to pouze trocha prace na vic ;)
edit : na víc V navíc ; ta cestina dela divy 8)
Offline
#20 29. 04. 2008 21:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Exponenciální / logaritmická rce/nerce
http://matematika.havrlant.net/forum/up … 0-dnes.jpg
- ano x "pro zuby" odpovida prave intervalum jak je v oficialnim vysledku (tedy x=-2, 2 klidne zustava, nema byt vylouceno, neni zadny duvod).
Nemusis venovat takovou pozornost nulovym bodum - to je jen takova pomucka pro odstraneni absolutni hodnoty. Pokud se chces ujistit, zda do intervalu vysledku patri a zrovna nejak vahas, tak, samozrejme dosad (jak navrhujes) a vidis, ze nerovnici vyhovuji. OK ?
Je to ale spise jen takove overeni. Stejne tak muzes prekontrolovat treba i jine cislo.
Prvni priklad je OK - postupujes spravne - pro definicní obor si overuji vzdy minimalne toto:
- vidim zlomek, jmenovatel nesmi byt 0,
- vidim log - vyraz za log (kolegove tomu rikaji "argument" :-) musi byt kladny,
- vidim odmocninu, arccos, arcsin ..... (nastesti, nevidim :-)
Vsak zkus dosadit 0, 4 a uvidis, ze budes nucen delit 0.
Kolegove plisna, aritentd, srdecne zdravim :-) mate pravdu, je to v poradku, co bych k tomu jeste rikala, ze :-)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální / logaritmická rce/nerce (TOTO TÉMA JE VYŘEŠENÉ)
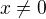 (neni tam
(neni tam 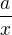 , ci
, ci 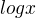 )
)
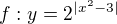 ma definicni obor D=R....je definovana pro vsechna realna x
ma definicni obor D=R....je definovana pro vsechna realna x