Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 01. 2011 12:33
poloha ťažiska
Nájdite polohu ťažiska drôtu ohnutého do tvaru písmena L s dlhšou stranou 20 cm a kratšou 10 cm.
nemozem pohnut s touto ulohou mohli by ste mi poradit akym sposobom mam najst suradnice taziska ? Skusal som cez sustavu hmotnych bodov ale to mi nevychadzalo spravne. (Aspon myslim) a pri ostatnych sposoboch som sa nevedel dopracovat k rieseniu. Ďakujem !!
Offline
#2 29. 01. 2011 12:39 — Editoval mikl3 (29. 01. 2011 12:45)
Re: poloha ťažiska
↑ trabant: těžiště bude určitě ležet mimo drát
(když zanedbáme hmotnost drátu) tak si to L doplníme na trojúhelník a potom těžiště určíme ne? nebo mi spíš řekni, jestli opravdu zanedbáváte hmotnost nebo jestli to máte řešit jinak
pokud jinak, tak materiál
Offline
#3 29. 01. 2011 12:52
Re: poloha ťažiska
No tie strany drotu bereme ako jednorozmerne teleso, teda ze ma len dlzku preto mam problem s tym ako urcit tazisko. Skusal som urcit tazisko jednej strany a potom druhej a najst na spojici ale neviem ci je to spravne . jedno tazisko by bolo 5 cm od zaciatku po osi x a druhe by bolo 10 cm od zaciatku po osi y (ak dame roh toho drotu do zaciatku suradnicovej sustavy). no a tezisko by malo byt na spojnici. Ale nie som si isty touto uvahou. preto by som chcel poradit. Co sa tyka hmotnosti tak ten drot berieme len ako geometricky utvar takze neviem.
Offline
#4 29. 01. 2011 12:55 — Editoval mikl3 (29. 01. 2011 12:57)
Re: poloha ťažiska
↑ trabant: vždyť jsem to psal, spoj si konce písmene L a budeš mít pravoúhlý trojúhelník, ve kterém budeš znát 3 strany, a jak najdeme Těžiště v trojúhelníku? v průsečíku těžnic
Odkaz
akorát, že to L nebude tak tlusté, ale bude to prostě trojúhelník
Offline
#5 29. 01. 2011 13:02
Re: poloha ťažiska
ja som ta pochopil ako to myslis ale ide mi skor o to (asi to bude suvisiet s tou hmotnostou) ze aj ta tretia strana ktoru som tam pridal ma na polohu taziska vplyv. To by znamenalo ze ked ju potom odstranim tak sa poloha taziska zmeni... mala by sa posunut smerom k zaciatku sustavy.
Offline
#6 29. 01. 2011 14:23
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: poloha ťažiska
↑ mikl3:
Těžiště rovinného útvaru (např. trojúhelníka) se přece nemusí shodovat s těžištěm jeho obrysu (třech stran trojúhelníka). I kdyby to ale platilo, tak tvému postupu nerozumím, můžeš to rozvést?
↑ trabant:
To je pravda, těžiště bude ležet na spojnici středů těch dvou úseček. Podle tvého značení: 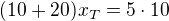 ,
, 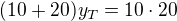
Offline
#7 29. 01. 2011 17:32 — Editoval [ReD]mikl (29. 01. 2011 17:33)
Re: poloha ťažiska
↑ FliegenderZirkus: ano, trojúhelník je rovinný útvar (Trojúhelník je rovinný geometrický útvar, mnohoúhelník se třemi vrcholy a třemi stranami.) což podle mě zní jasně těžiště obrysu je to samé jako těžiště trojúhelníka (což by byla dobrá debata, co to je obrys trojúhelníku a co trojúhelník) protože trojúhelník nemá hmotný obrys
máme pravý úhel a délky dvou úseček, doplníme si to na trojúhelník a těžiště je jasné
a i kdyby ne, máme úsečky svírající pravý úhel, udělejme si úsečky spojující konce ramen tohoto úhlu (konce stran) se středy stran protilehlých
to je to samé jako těžnice v trojúhelníku, protože na průnik nám stačí 2 a ty my máme...
nejde o to, že to má hmotnost, tu zanedbáváme, zkus si představit nehmotné písmeno L (náš objekt) konce písmene L zavěsit na nějaký bodec, ze kterého je k zemi spuštěna olověnka... je to jasné
Offline
#8 29. 01. 2011 17:41
Re: poloha ťažiska
↑ [ReD]mikl: ten příspěvěk jsem psal já, nevěděl jsem, že mám druhý účet, napsal jsem to blbě, myslel jsem to takhle: představme si to jako nehmotnou věc, když zavěsíme konec písmene na olověnku, tak nám ukáže těžnici (třeba si uděláme rysku na té druhé straně, kde se protne) poté zavěsíme z druhého konce a upět těžnice bude procházet středem delší strany (pokud jsme si prvně zavěšovali z vrcholu delší)
tohle je mé řešení a úvaha, samozřejmě se mohu mýlit...
Offline
#9 29. 01. 2011 18:06
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: poloha ťažiska
↑ mikl3:
Existují dvě abstrakce - modely reality. Jednou je tenká deska (s plošnou hustotou), druhou tenký drát (s délkovou hustotou). Můžu vyříznout kus desky ve tvaru trojúhelníka, nebo ohnout drát do tvaru trojúhelníka a tyto případy je nutné rozlišovat. Ve skutečnosti samozřejmě vždy půjde o trojrozměrné útvary s prostorovou hustotou.
[ReD]mikl napsal(a):
↑ FliegenderZirkus:
nejde o to, že to má hmotnost, tu zanedbáváme, zkus si představit nehmotné písmeno L (náš objekt) konce písmene L zavěsit na nějaký bodec, ze kterého je k zemi spuštěna olověnka... je to jasné
Bohužel mi to jasné není :-) Tady už se dostáváme k rozdílu mezi těžištěm a hmotným středem, ale v obou případech myslím musím uvažovat nějakou nenulovou hustotu (a tedy i hmotnost) předmětu, jinak by přece ty pojmy neměly smysl...
Offline
#10 29. 01. 2011 18:17
Re: poloha ťažiska
↑ FliegenderZirkus: děkuji za debatu, ano, v realitě to jsou trojrozměrné objekty, ty modely abstrakce se mi sem nějak nehodí (chápu je, ale zapomeňmě na jakoukoliv hustotu a třetí rozměr)
když si představíme čistě geometricky písmeno L (nevím, zda si ho můžeme doplnit na trojúhelník, také v tomhle případě zapomenu na to zavěšování, nemáme hmotnost), chápu ty těžiště stran ale jak potom najdeme přesné těžiště? mě právě napadlo spojit si konce písmen s osou protilehlé strany (jakoby v trojúhelníku) a to poté udělat i s druhým koncem písmene, uděláme tak dvě těžnice v "neexistujícím" trojúhelníku
zkusím to popsat lépe: máme trojúhelník pravoúhlý ABC (pravý úhel u vrcholu B), středy stran jsou po řadě pojmenovány EFG, nyní udělejme těžnice Ta a Tc (Tb ne, stačí nám 2)
no a nyní máme písmeno L které je ten trojúhelník bez přepony (kterou jsme stejně pro ty 2 těžnice nepotřebovali) nebylo by to tak možné?
Offline
#11 29. 01. 2011 18:25
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: poloha ťažiska
↑ mikl3:
Tímhle postupem dostaneme těžiště trojúhelníkové desky, které je ovšem jinde než těžiště trojúhelníkového drátu a už úplně jinde než těžiště drátu ve tvaru písmene L.
Offline
#12 29. 01. 2011 18:35
Re: poloha ťažiska
↑ FliegenderZirkus:Tak se odvolam na tvoji metodu a placnu nebude teziste v pomeru1:2 na té spojnici?
Offline
#13 29. 01. 2011 19:02
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: poloha ťažiska
↑ mikl3:
Jj s tím souhlasím
Offline