Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 02. 2011 19:41
- check_drummer
- Příspěvky: 4952
- Reputace: 106
Nemožnost vyjádření sumy v uzavřeném tvaru
Je známo, že 1+2+...+n=n.(n+1)/2, tj. uvedenou sumu lze vyjádřit v uzavřeném tvaru (neformálně a ne zcela přesně řečeno "vzorcem"). Pojem "uzavřený tvar" by bylo možno nějak formalizovat - např. že obsahuje pouze jisté funkce (mocnina, 1/x, elementární funkce), které je možné skládat, požít funkce inverzní, násobit a sčítat, obsahuje proměnnou n a libovolné číselné konstanty, apod.
Existuje nějaká suma výrazů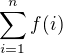 
, že tuto sumu napak není možné vyjádřit v uzavřeném tvaru - a lze to i dokázat? (Každý výraz f(i) nechť naopak nějakým uzavřeným tvarem je.)
"Máte úhel beta." "No to nemám."
Offline
#2 06. 04. 2011 21:16
Re: Nemožnost vyjádření sumy v uzavřeném tvaru
V podstatě se hledá analogie "nezintegrovatelných" funkcí, chápu to správně?
Neznám úplně podrobnosti, ale myslím, že by to mohla splňovat harmonická čísla.
Offline
#3 08. 06. 2011 20:59
- check_drummer
- Příspěvky: 4952
- Reputace: 106
Re: Nemožnost vyjádření sumy v uzavřeném tvaru
↑ Olin:
V podstatě ano, ale nevím, zda tato analogie v něčem pomůže.
(Pardon, všiml jsem si až teď, že jsi odpověděl, občas mi čtvereček nového příspěvku nějak záhadně zmizí.)
"Máte úhel beta." "No to nemám."
Offline