Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 02. 2011 21:45
Nejmenší perioda funkce..
Zdravim, mam problem s vyresenim nasledujiciho zadani: Nejmensi perioda funkce: y= tgx/3 spravny vysledek by mel byt 3pí/2
absolutne nevim jak postupovat pri reseni tohoto prikladu, predem dekuji za spravny postup
ps: nevim jak se pise pí nebo-li 3,14....
Offline
- (téma jako vyřešené označil(a) Mat.Satan)
#2 11. 02. 2011 22:09 — Editoval Dana1 (11. 02. 2011 22:14)
- Dana1
- Host
Re: Nejmenší perioda funkce..
↑ Mat.Satan:
Ak je za tg (x/3), perióda je asi 3pí, zdá sa, že aj wolfram to hovorí tu
Zistila som nulové body x/3 = 0 + k*pí / *3,
x = 3k*pí ... a z toho je vzdialenosť medzi rovnakými hodnotami (perióda) rovná 3pí, k je celé číslo (myslím)
#4 12. 02. 2011 01:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nejmenší perioda funkce..
↑ Mat.Satan:
Obecně nejmenší periodu funkce f najdeš tak, že řešíš rovnici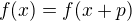 ,
,
která ovšem musí platit pro každé x z definičního oboru. Zde tedy řešíme rovnici
(1) 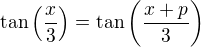 .
.
Tato rovnice musí platit pro všechny x z definičního oboru, takže dosadíme třeba x=0. ,
,
kde k je celé číslo. Tím máme dostatečně omezené p, nemusíme už rovnici (1) řešit pro další x, protože vezmeme to nejmenší přípustné kladné p (to je  ) a snadno ověříme, že rovnice (1) s tímto p platí pro každé x z definičního oboru. Nalezli jsme tak nejmenší periodu.
) a snadno ověříme, že rovnice (1) s tímto p platí pro každé x z definičního oboru. Nalezli jsme tak nejmenší periodu.
Offline
#6 12. 02. 2011 08:13
Re: Nejmenší perioda funkce..
↑ Pavel Brožek:
dekuju za vyresni a omlouvam se, sptane jsem se podival na spravny vysledek ma to byt 3pí ;)
Offline
#7 12. 02. 2011 08:15
- Dana1
- Host
Re: Nejmenší perioda funkce..
↑ Mat.Satan:
Ak si spokojný, uzavri prosím Ťa, tému (pri prvom príspevku vpravo dolu). Ďakujem.
#8 12. 02. 2011 08:21
Re: Nejmenší perioda funkce..
↑ Pavel Brožek:
jeste jsem se chtel zeptat kdyz jste postupne resil rovnici tak nechapu jak jste dosel k p/3=kpí
Offline
#9 12. 02. 2011 08:25
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nejmenší perioda funkce..
↑ Mat.Satan:
Řešení rovnice 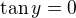 je
je 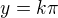 , kde k je celé číslo. Pokud to nevidíš rovnou, můžeš si to ještě rozepsat:
, kde k je celé číslo. Pokud to nevidíš rovnou, můžeš si to ještě rozepsat: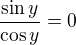
Aby byl zlomek roven nule, musí být jeho čitatel rovný nule (a zároveň to musí být definované, což zde není problém, protože pokud má být sinus nulový, pak cosinus je určitě nenulový). Dostáváme tak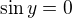
Tady už bys měl vědět, že řešení je 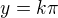 . A pro nás pak
. A pro nás pak 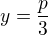 .
.
Offline
#10 09. 03. 2014 14:20 — Editoval xdobia09 (09. 03. 2014 14:20)
Re: Nejmenší perioda funkce..
Dobrý den,
mám podobný příklad a i podle popsaných postupů se nemohu dostat k výsledku: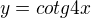
První krok:
Jenže cotg 0 přece není definován, to už je něco špatně mám takový pocit. Stejně tak nerozumím tomu když Pavel Brožek udělal tento krok 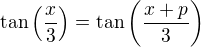 . jakto že v čitateli není 3p ... přece po dosazení bych ke zlomku x/3 musel přičíst p/1.
. jakto že v čitateli není 3p ... přece po dosazení bych ke zlomku x/3 musel přičíst p/1.
Díky za pomoc
Offline
#12 09. 03. 2014 18:03
- janca361

- .
- Příspěvky: 3284
Re: Nejmenší perioda funkce..
↑ xdobia09:
Zdravím,
a nebylo by lepší si založit vlastní téma podle pravidel s případným odkazem na toto téma?
A ano, právě z důvodu označení za vyřešené si nikdo tématu nevšiml.
Offline
#13 09. 03. 2014 18:09
Re: Nejmenší perioda funkce..
↑ janca361:
To jsem udělal, byl jsem odkázán na to, že zde se to již řešilo :)
Offline
#15 09. 03. 2014 18:20 — Editoval coolcake (09. 03. 2014 18:21)
Re: Nejmenší perioda funkce..
↑ xdobia09: Ahoj, ja to nerobím cez tie rovnice, proste... vždy keď je pred x nejaké číslo ako napr 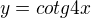 Tak tá 4 znamená vlastne, že perióda bude 4 krát menšia. :) Pri takýchto jednoduchých by ti to mohlo úplne vystačiť. Keď sa pozrieš na jednotkovú kružnicu, tak to aj pochopíš, že ten napr, keď dosadíš uhol 30^\circ do
Tak tá 4 znamená vlastne, že perióda bude 4 krát menšia. :) Pri takýchto jednoduchých by ti to mohlo úplne vystačiť. Keď sa pozrieš na jednotkovú kružnicu, tak to aj pochopíš, že ten napr, keď dosadíš uhol 30^\circ do 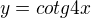 tak je to hodnota
tak je to hodnota 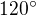 , čiže ako keby si 4 krát rýchlejšie obehol jednotkovú kružnicu a tým pádom aj perióda sa ti skráti...
, čiže ako keby si 4 krát rýchlejšie obehol jednotkovú kružnicu a tým pádom aj perióda sa ti skráti...
Demonštrácia: 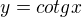 má periódu
má periódu 
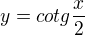 má periódu 2
má periódu 2 Atď....
Atď....
Easy na zapamätanie! :)
Edit, ak sa naučíš periódu pre všetky základné goniometrické funkcie, tak cez tieto hrátky sa rýchlo dopracuješ ku všetkému.
Čím viac človek vie, tým viac vie, že nevie...
Offline
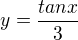 pak je perioda
pak je perioda