Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 17. 02. 2011 21:27 — Editoval claudia (17. 02. 2011 21:38)

claudia
Richard P. Feynman
Příspěvky: 478
Reputace:   41 
 

limita: Příklady z matematiky pro fyziky I, 3.1.41

Dobrý večer,

počítám příklady ze sbírky a nevychází mi autorský výsledek. Zadání je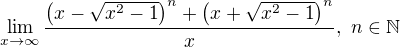

$\lim_{x \rightarrow \infty} \frac{\(x-\sqrt{x^2-1}\)^n + \(x+\sqrt{x^2-1}\)^n}{x},\ n\in \mathbb{N}$

a jako řešení je psáno 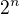$2^n$.

Můj postup je:

$\lim_{x \rightarrow \infty} \frac{\(x-\sqrt{x^2-1}\)^n + \(x+\sqrt{x^2-1}\)^n}{x} =\nl = \lim_{x \rightarrow \infty} \frac{\(x-\sqrt{x^2-1}\)^n}{x} + \lim_{x \rightarrow \infty}  \frac{\(x+\sqrt{x^2-1}\)^n}{x} =\nl = \lim_{x \rightarrow \infty} \frac{1}{x}\(\frac{x^2-x^2+1}{x+\sqrt{x^2-1}}\)^n + \lim_{x \rightarrow \infty} \frac{\(x+\sqrt{x^2-1}\)^n}{x}=\nl =\frac{1}{\infty}\frac{1}{\infty+\infty} + \lim_{x \rightarrow \infty} \frac{\(x+\sqrt{x^2-1}\)^n}{x}=\nl =\lim_{x \rightarrow \infty} \frac{\(x+\sqrt{x^2-1}\)^n}{x}$

Nyní pro n=1:
$\lim_{x \rightarrow \infty} \frac{\(x+\sqrt{x^2-1}\)^n}{x} =\lim_{x \rightarrow \infty} \frac{x+\sqrt{x^2-1}}{x} = 2 = 2^n$

Ovšem pro n>1:
$\lim_{x \rightarrow \infty} \frac{\(x+\sqrt{x^2-1}\)^n}{x}\nl = \lim_{x \rightarrow \infty} \frac{\sum_{a=0}^n\(x^a\(x^2-1\)^{\frac{n-a}2}\)}{x}\nl = \lim_{x \rightarrow \infty} \sum_{a=0}^n\(\binom{n}{a}x^{a-1}\(x^2-1\)^{\frac{n-a}2}\)\nl = \sum_{a=0}^n\lim_{x \rightarrow \infty} \(\binom{n}{a}x^{a-1}\(x^2-1\)^{\frac{n-a}2}\)\nl = \sum_{a=0}^n\lim_{x \rightarrow \infty} \(\binom{n}{a}x^{a-1}\(x^2\(1-\frac{1}{x^2}\)\)^{\frac{n-a}2}\)\nl = \sum_{a=0}^n\lim_{x \rightarrow \infty} \(\binom{n}{a}x^{a-1}x^{n-a}\(1-\frac{1}{x^2}\)^{\frac{n-a}2}\)\nl = \sum_{a=0}^n\lim_{x \rightarrow \infty} \(\binom{n}{a}x^{n-1}\(1-\frac{1}{x^2}\)^{\frac{n-a}2}\)\nl = \lim_{x \rightarrow \infty} x^{n-1} \sum_{a=0}^n \binom{n}{a}\lim_{x \rightarrow \infty} \(1-\frac{1}{x^2}\)^{\frac{n-a}2}\nl = \infty \sum_{a=0}^n \binom{n}{a} = \infty \neq 2^n$

Prosím o odhalení chyby v mém výpočtu nebo potvrzení jeho správnosti. Děkuji.

Pište prosím své dotazy srozumitelně a v TeXu (Detexify). Píšete je jen jednou, ale my je čteme mnohokrát. Čím méně času strávím luštěním vaší otázky, tím více mi zbyde na její zodpovězení.

Offline

  • (téma jako vyřešené označil(a) claudia)

#2 17. 02. 2011 21:40 — Editoval Cynyc (17. 02. 2011 21:44)

Cynyc
Příspěvky: 175
Reputace:   16 
 

Re: limita: Příklady z matematiky pro fyziky I, 3.1.41

↑ claudia:Ten výpočet je zbytečně složitý, ale správný. Autorský výsledek je chybný, podle mého autor zapomněl v zadání ve jmenovateli umocnit x na n-tou. A jinak stačí

Offline

 

#3 17. 02. 2011 21:41 — Editoval FailED (17. 02. 2011 21:44)

FailED
Příspěvky: 1255
Reputace:   42 
 

Re: limita: Příklady z matematiky pro fyziky I, 3.1.41

↑ claudia:

Ahoj,
postup vypadá dobře, problém by řešilo, kdyby v zadání bylo ve jmenovateli 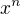$x^n$.

Místo binomické věty je možné přímo vytknout a krátit, tedy

$\frac{\(x+\sqrt{x^2-1}\)^n}{x}=\frac{x^n\(1+\sqrt{1-\frac{1}{x^2}}\)^n}{x}$.

Offline

 

#4 17. 02. 2011 21:48 — Editoval claudia (17. 02. 2011 21:50)

claudia
Richard P. Feynman
Příspěvky: 478
Reputace:   41 
 

Re: limita: Příklady z matematiky pro fyziky I, 3.1.41

Děkuji, někdy mi dělá problém vidět snadné věci :-) Pro to x^n to zjevně sedí:
$\lim_{x \rightarrow \infty} x^{n-n} \sum_{a=0}^n \binom{n}{a}\lim_{x \rightarrow \infty} \(1-\frac{1}{x^2}\)^{\frac{n-a}2} = 1 \sum_{a=0}^n \binom{n}{a} = 2^n$
(a dokonce též i bez binomické věty :-)

Pište prosím své dotazy srozumitelně a v TeXu (Detexify). Píšete je jen jednou, ale my je čteme mnohokrát. Čím méně času strávím luštěním vaší otázky, tím více mi zbyde na její zodpovězení.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson