Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 02. 2011 12:26
Re: Znovu geometria + logika
11) Napadá mě zatím jen postup, prostě to zkusit, takže když dělíme dvojkou, tak zbytek po dělení 37 bude 1 a zbytek po dělení 47 bude taky 1. Číslo 2 tedy zadání vyhovuje. Můžeš zkusit další, zas tak moc jich není..
Vesmír má čas.
Offline
#3 18. 02. 2011 12:48 — Editoval Hudler (18. 02. 2011 13:19)
Re: Znovu geometria + logika
12) Objem jehlanu se spočítá

Musíš najít pravoúhlý trojúhelník kde budeš znát stranu a úhel a pomocí goniometrikých fcí dopočítáš v. Napadá tě jak bude takový trojúhelník vypadat?
13) Najdi průsečíky rovnoběžek s přímkamy 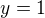 a
a  , nakresli (představ si) si obrázek a obsah rovnoběžníku vypočítej pomocí vzorce
, nakresli (představ si) si obrázek a obsah rovnoběžníku vypočítej pomocí vzorce 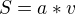
Offline





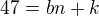 odečtením
odečtením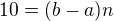
 dělí desítku.
dělí desítku.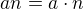 např.
např. 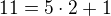 , a=5, n=2, k=1
, a=5, n=2, k=1 má stejnou úlohu jako
má stejnou úlohu jako  , jen u druhého čísla musí být jiné písmenko.
, jen u druhého čísla musí být jiné písmenko.