Matematické Fórum

hmyzak · 14. 04. 2009 20:48

↑↑ kaja.marik:

díky

Stejky · 09. 05. 2009 16:54

Mohl by někdo ukázat postup vypočtení těch průsečíků s osami z rovnice tečny? Není mi to jasné... díky

kaja(z_hajovny) · 09. 05. 2009 21:12

1. dosadim x=0 a vypocitam y
2. dosadim y=0 a vypocitam x

Stejky · 09. 05. 2009 22:19

A jak vypadá ta rovnice tečny? Protože nejspíše používám nesprávnou . děkuji

kaja(z_hajovny) · 09. 05. 2009 23:48

viz prispevek cislo 25

Stejky · 10. 05. 2009 08:02 — Editoval Stejky (10. 05. 2009 08:03)

Ale to furt nevychází krucinál. Furt počítám a nedojde k výsledku co je na předešlé straně.
rovnice tecny: 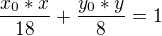$\frac{x_0*x}{18}+\frac{y_0*y}{8}=1$ .
Z toho mi vyjde : $x_0=\frac{18}{x}$ a $y_0=\frac{8}{y}$ .
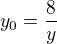A teď dosadím x0 místo x do rovnice elipsy: $\frac{x^2}{18}+\frac{y^2}{8}=1$ a sice $\frac{(\frac{18}{x})^2}{18}+\frac{y_0^2}{8}=1$ .
A z toho si mám vyjádřit y0. Jenže ať dělám co dělám, nevyjádřím ho stejně jako na předešlé stránce. Dělám někde chybu?

kaja(z_hajovny)

pokud je bod [x_0,y_0] na elipse, tak bod s x-ovou souradnici 18/x0 jiste lezi mimo elipsu, to jde videt i z obrazku (prusecik tecny s osami je hodne bokem od elipsy)
takze tohle dosazeni je odsouzeno k nezdaru hned na zacatku

ctete psispevek 7

Matematické Fórum

#26 14. 04. 2009 20:48

Re: extrémy

#27 09. 05. 2009 16:54

Re: extrémy

#28 09. 05. 2009 21:12

Re: extrémy

#29 09. 05. 2009 22:19

Re: extrémy

#30 09. 05. 2009 23:48

Re: extrémy

#31 10. 05. 2009 08:02 — Editoval Stejky (10. 05. 2009 08:03)

Re: extrémy

#32 10. 05. 2009 10:53 — Editoval kaja(z_hajovny) (10. 05. 2009 10:56)

Re: extrémy

Zápatí