Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 02. 2011 18:13
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Maximální řád prvku v grupě s k generátory
Ahoj,
nechť minimální počet generátorů nějaké grupy G je k (tj. existuje k prvků z G, které generují G, ale žádných k-1 prvků G negeneruje). Nechť |G|=n. Označme r(g) řád prvku g z G (tj. počet prvků podgrupy G generované prvkem g). Označme m=max{r(g); g z G}. Existuje potom nějaký netriviální horní a/nebo dolní odhad pro hodnotu m (např. v závisosti na n,k, případně na nějakých dalších "veličinách")?
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#2 27. 11. 2011 03:09
Re: Maximální řád prvku v grupě s k generátory
Offline
#3 27. 11. 2011 09:34
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
"Máte úhel beta." "No to nemám."
Offline
#4 27. 11. 2011 11:51
Re: Maximální řád prvku v grupě s k generátory
Offline
#5 07. 12. 2011 20:20 — Editoval vanok (08. 12. 2011 02:56)
Re: Maximální řád prvku v grupě s k generátory
Ahoj ↑ check_drummer:,
Studoval si pripad cyclickych grup (ine meno monogena grupa)?
Tieto groupy su generovane jednym prvkom...
Mozno toto
by ta mohlo zaujimat, i ked to neodpoveda na tvoj problem.
na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 14. 12. 2011 10:12
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer:,
Ak chces mozme tu zacat studovat dost blizky problem co chces studovat cf↑ check_drummer:
generatory konecnych abelovskych grup(cize komutativnych)
Je to v teorii grup ist ako po autostrade ... a az potom zacat vseobecne studium generatov vseobecnych grup.
Co si o tom myslis?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 14. 12. 2011 15:19
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Zdravím členy fóra,
pokusím se vyjádřit konkrétněji co nejdřív, ale úloha, kterou ↑ check_drummer: uvedl, je mi povědomá.
Pamatuji si, že se pro šetření takových otázek zaváděly určité funkce.
Téma je průřezově zpracováno zde.
Asi nebudu mít večer moc času, ještě uvidím.
Offline
#8 14. 12. 2011 20:03
Re: Maximální řád prvku v grupě s k generátory
↑ constr:,
To ma zaujima.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 14. 12. 2011 20:47
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Určitě je přínosné začít od specifického a pokračovat k obecnému. Lze obecně generátory abelovských grup nějak charakterizovat, či je dokonce pro každou abelovskou grupu nějak jednoduše určit?
"Máte úhel beta." "No to nemám."
Offline
#10 14. 12. 2011 22:14 — Editoval vanok (27. 12. 2011 18:46)
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer: a vsetci iny,
O KOMUTATIVNYCH KONECNYCH GRUPACH
UVOD
Tu ukazeme pre komutitavne konecne grupy 3 teoremy o dekompozicii komutativnej konecnej grupy G
*na p-grupy (nie povinne cyklicke)
*na cyklicke p-grupy
*na cyklicke grupy 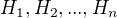 take ze rad
take ze rad 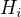 deli rad
deli rad pre
pre 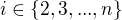
Prva teorema co nas informuje o dekompozicii komutativnej konecnej grupy G na p-grupy (nie povinne cyklicke)  : p-zlozky grupy G (Rad
: p-zlozky grupy G (Rad  sa da vyjadrit ako funkcia radu
sa da vyjadrit ako funkcia radu  ...to doplnim neskor) je
...to doplnim neskor) je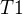 teorema 1
teorema 1
Kazda komutativna konecna grupa G je priamy sucet (somme directe) p-grup  na mnozine prvociselnych delitelov
na mnozine prvociselnych delitelov  radu grupy
radu grupy  :
:
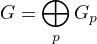
*****
Pred dokazom precitajte vsetko az do po cvicenie 9). Veta 1
 nam posluzi v dokaze teoremy 1
nam posluzi v dokaze teoremy 1 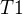
Term p-grupa, znamena ze vsetki prvky takej grupy maju periodu, nejaku mocninu p (p>0 prvocislo).
PRIKLADY:
 je 2-grupa radu 4.
je 2-grupa radu 4.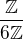 nie je p-grupa, ma prvky radu 2, 3 alebo 6
nie je p-grupa, ma prvky radu 2, 3 alebo 6Klein-ova grupa
 je 2-grupa radu 4
je 2-grupa radu 4Cvicenia:
1)Je
 jedna p-grupa?
jedna p-grupa?2)Existuju aj nekonecne p-grupy?
3)Pre ktore
 ,
, 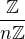 je p-grupa?
je p-grupa?*****
POJEM:priamy sucet (somme directe)
Nech
 je komutitavna aditivna groupa a nech
je komutitavna aditivna groupa a nech ,
,  ,...a
,...a  su podgrupy grupy
su podgrupy grupy  .
. je priamy sucet podgrup
je priamy sucet podgrup 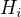 ak kazdy prvok
ak kazdy prvok 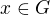
sa pise JEDNOZNACNE
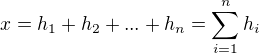
kde
 .
.To sa pise
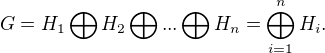
PRIKLADY:
Pre kazde
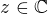 mame jednoznacne
mame jednoznacne  kde
kde 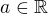 a
a  .
. 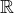 a
a 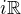 su aditivne podgrupy grupy
su aditivne podgrupy grupy  a
a
V
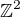 , polozme
, polozme 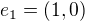 a
a 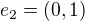 .
.Tak mame
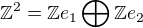
Cvicenie:
4) Pre prirodzene cislo
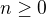 a
a ![kopírovat do textarea $\mathbb{C}_n[X] $](/mathtex/23/238deef08e1b0e9085ed8673b23e03b1.gif) aditivna grupa polynomov, z komplexniny koeficientamy, najviac stupna
aditivna grupa polynomov, z komplexniny koeficientamy, najviac stupna 
Polozme
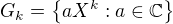 .
.Dokazte ze
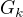 je aditivna podgrupa grupy
je aditivna podgrupa grupy ![kopírovat do textarea $\mathbb{C}_n[X] $](/mathtex/23/238deef08e1b0e9085ed8673b23e03b1.gif) ;
;a ze
![kopírovat do textarea $\mathbb{C}_n[X] $](/mathtex/23/238deef08e1b0e9085ed8673b23e03b1.gif) je priamy sucet grup
je priamy sucet grup 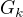 .
.Teraz tu ukazeme aka je relacia medzi "priamov sumov" a "sumov" podgrup nejakej grupy
 veta 1
veta 1Aditivna grupa
 je priamy sucet jej podgrup
je priamy sucet jej podgrup  ,
,  ,...a
,...a  len a len ked
len a len keda)

b)

Dokaz: cvicenie 5)
Tato veta je uzitocna na dokaz
 , teoremy1
, teoremy1cvicenie 6) Sucet
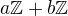 kde
kde 
nie je nikdy priamy.
*****
Pre
 prvocislo take ze deli rad nejakej grupy
prvocislo take ze deli rad nejakej grupy  ,
,mnozina
 prvkov z
prvkov z  ktorych rad je nejaka mocnina z
ktorych rad je nejaka mocnina z  je podgrupa grupy
je podgrupa grupy  ; a vola sa p-zlozka grupy
; a vola sa p-zlozka grupy  .
.Priklad:
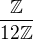 ma 2-zlozku
ma 2-zlozku 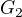 a 3-zlozku
a 3-zlozku 
take ze :
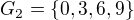

Cvicenie 7)
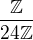 )
)Cvicenie 8) Dokazte ze
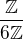 je priamy sucet jej p-zloziek.
je priamy sucet jej p-zloziek.Cvicenie 9) Ako to je z
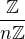 ?
?**********
Teraz sa vratme k
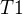
Tato teorema je existecna teorema rozkladu na p-grupy, a vdaka nej mozeme povedat, ze nejaka konecna komutativna grupa
 , radu
, radu 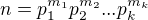 je taka ze
je taka ze 
PRIKLAD:
Cize vdaka
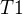 mozme pisat ze na priklad
mozme pisat ze na priklad 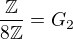
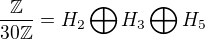
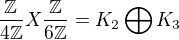
uz pred tym ako sme uplne urcili grupy

Tento vysledok nam moze casto byt uzitocny:

Este jedno riesene cvicenie.
Cvicenie 10)
 nam da ze
nam da ze 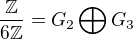

co znamena:
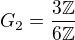 a je izomorfne z
a je izomorfne z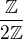
Podobne
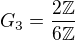 a je izomorfne z
a je izomorfne z
Z toho mame:
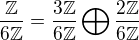
Poznamka: isomorfizmy medzi
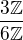 a
a 
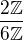 a
a 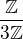
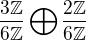 a
a 
nam daju len ze
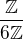 je izomorfne z
je izomorfne z 
Mozte studovat podrobne vsetki tieto izomorfismy.
Je uzitocne porozmyslat aky je rozdiel medzi rovnostou a izomorfizmom grup.
**********************************************************
Pozrime sa teraz na konecne cyklicke grupy.
Bud
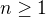 cele cislo, take:
cele cislo, take: 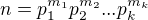 je rozklad n na primarne faktory a nech
je rozklad n na primarne faktory a nech  radu n, ( cize
radu n, ( cize  )
)Pre
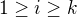 , polozne
, polozne  zlozku p_i-primarnu grupy
zlozku p_i-primarnu grupy  . Dokazme, ze rad
. Dokazme, ze rad  je
je  .
.Akoze
 je cyklicka, existuje podgroupa
je cyklicka, existuje podgroupa  grupy
grupy  ze jej rad je
ze jej rad je  .
.****************************
Poznamka Tuto temu(komutativna konecna grupa) budem doplnovat v tomto ramecku ...pre lepsiu citatelnost.
Najprv tu dam tri teoremy o dekompozicii a az potom dopl \innim ich dokazy.
Tieto riadky su podla mojich osobnych poznamok z roznych prednasok,seminarov, diskusii z kolegmy .... literaturu dam na konci tohoto projektu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 15. 12. 2011 13:00
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
vanok napsal(a):
Term p-grupa, znamena ze vsetki prvky takej grupy maju periodu, nejaku mocninu p.
priklady:je 2-grupa radu 4.
Tedy p je dle definice prvočíslo?
Uvažujeme grupy 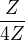 s operací "+" nebo s jinou operací?
s operací "+" nebo s jinou operací?
Periodou je zde myšlena libovolná perioda nikoli nejmenší, že? Např. prvek 0 má (pokud se jedná o grupy se sčítáním) periodu 1, ovšem tedy i kteroukoliv další vyšší, že?
"Máte úhel beta." "No to nemám."
Offline
#12 15. 12. 2011 14:10
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer:
Dakujem.
Prva poznamka:
ano p je prvocislo, dal som to explicitne do definicie
Tvoja druha poznamka:MAS ZASA PRAVDU
Term p-grupa, znamena ze vsetki prvky takej grupy maju periodu, nejaku mocninu p (p>0 prvocislo).
ze medzi ich periodami je jedna taka ako ze...
Prave to bol problem pre mna, ako to napisat aby aj neutralny prvok bol v tom.....
Pridam, prioritne, pred tym ako pojdem dalej aj pojem priamej sumy ( a tiez overim ci sa tento vyraz v Cz a Sk pouziva)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 15. 12. 2011 21:57
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Ke cvičení 1) V 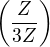 mají prvky řád 1 nebo 3 a v
mají prvky řád 1 nebo 3 a v  mají prvky řád 1,3 nebo 9 (tipuji), přičemž řád 1 nastane jen u prvků 0. Takže pro (i,j) j=0 máme řád 1 nebo 3 a pro j<>0 máme řád 3 nebo 9 (řád prvku v grupě dané první složkou dělí řád prvku v grupě dané druhou složkou). Takže dle mého jde o 9-grupu řádu 27. Snad jsem tu úvahu moc neodbyl a něco neopomenul.
mají prvky řád 1,3 nebo 9 (tipuji), přičemž řád 1 nastane jen u prvků 0. Takže pro (i,j) j=0 máme řád 1 nebo 3 a pro j<>0 máme řád 3 nebo 9 (řád prvku v grupě dané první složkou dělí řád prvku v grupě dané druhou složkou). Takže dle mého jde o 9-grupu řádu 27. Snad jsem tu úvahu moc neodbyl a něco neopomenul.
"Máte úhel beta." "No to nemám."
Offline
#14 15. 12. 2011 22:07
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Ke cvičení 2) co třeba vyjít ze cvičení 1) a sestrojit např.: 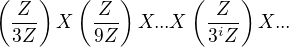
"Máte úhel beta." "No to nemám."
Offline
#15 15. 12. 2011 23:42 — Editoval vanok (16. 12. 2011 01:38)
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer:,
cvicenie 1).
Nie 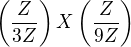 je 3-grupa... podla definicie vysie.
je 3-grupa... podla definicie vysie.
Vsetki prvky maju rad nejaku mocninu 3roch
cvicenie 2)
Ano je to dobra myslienka... potrebuje to len trochu viac formalizovat.
Dam trochu iny priklad:
Polozme  kde
kde 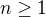
Prvky 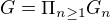 su postupnosti
su postupnosti 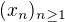 ,
,
polozme  .
.
G s tymto zakonom je nekonecna 5-grupa.
Zda sa mi ze si chcel urobit nieco podobne.
pridal som cvicenie 3)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 16. 12. 2011 07:41
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Ano, pardon, je to 3-grupa nikoli 9-grupa (9 je už mocnina 3).
K té konstrukci - Tvá je jednodušší - "opakuješ" v kartézském součinu stejnou strukturu, ta moje je komplikovanější a důkaz, zda je to p-grupa, by byl složitější (pokud to vůbec p-grupa je).
"Máte úhel beta." "No to nemám."
Offline
#17 16. 12. 2011 07:42
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Ke cvičení 3 - takhle bez přemýšlení bych řekl, že pro n, která jsou mocninou nějakého prvočísla.
"Máte úhel beta." "No to nemám."
Offline
#18 16. 12. 2011 12:16
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer:,
Ano, dobra intuicia, a mozes urobit dokaz...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 16. 12. 2011 13:12 — Editoval constr (18. 12. 2011 23:54)
Re: Maximální řád prvku v grupě s k generátory
Řešením pro konečné komutativní grupy je  tedy řád Sylowovy p-podgrupy.
tedy řád Sylowovy p-podgrupy.
- na základě věty o primárním cyklickém rozkladu modulů (kde obor hlavních ideálů se položí 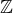 ) a definice Sylowovy grupy.
) a definice Sylowovy grupy.
Nechť řád grupy  je
je  , přičemž druhý činitel
, přičemž druhý činitel  je s
je s  nesoudělný. Protože každá konečná p-grupa má za řád určitou mocninu
nesoudělný. Protože každá konečná p-grupa má za řád určitou mocninu 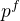 , musí každá p-grupa, která je podgrupou grupy
, musí každá p-grupa, která je podgrupou grupy  , mít za řád určitého dělitele mocniny
, mít za řád určitého dělitele mocniny 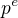 . Potom p-grupa
. Potom p-grupa  s maximálním možným řádem
s maximálním možným řádem 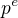 se nazývá Sylowova p-podgrupa grupy
se nazývá Sylowova p-podgrupa grupy  . Z této definice vyplývá, že grupa
. Z této definice vyplývá, že grupa 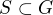 je Sylowova p-podgrupa grupy
je Sylowova p-podgrupa grupy  právě tehdy, když řád grupy
právě tehdy, když řád grupy  je mocninou prvočísla
je mocninou prvočísla  a index
a index ![kopírovat do textarea $[G:S]$](/mathtex/fd/fd29ab9b2657ae0eb2b9ed52c162049e.gif) je s
je s  nesoudělný.
nesoudělný.
Z věty o cyklickém rozkladu, kterou uvádí ↑ vanok: vyplývá, že konečná komutativní grupa  je izomorfní direktní sumě
je izomorfní direktní sumě 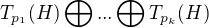 konečného počtu podgrup p-grupy
konečného počtu podgrup p-grupy 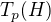 .
.
Každý faktor 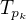 je
je 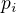 -podgrupa, takže jeho řád je nějaká mocnina
-podgrupa, takže jeho řád je nějaká mocnina  . Tedy řád grupy
. Tedy řád grupy  je
je  . To ukazuje, že k-tice prvočísel
. To ukazuje, že k-tice prvočísel 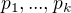 obsahuje všechny prvočíselné dělitele čísla
obsahuje všechny prvočíselné dělitele čísla  . Z toho vyplývá, že každá podgrupa
. Z toho vyplývá, že každá podgrupa 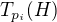 je Sylowova
je Sylowova 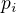 -podgrupa grupy
-podgrupa grupy  . Tato podgrupa byla definovaná tak, že obsahuje všechny prvky grupy
. Tato podgrupa byla definovaná tak, že obsahuje všechny prvky grupy  , jejichž řád je nějaká mocnina
, jejichž řád je nějaká mocnina 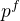 , tedy musí obsahovat každou
, tedy musí obsahovat každou 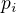 -podgrupu grupy
-podgrupu grupy  . Speciálně
. Speciálně 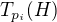 je jediná
je jediná 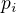 -podgrupa řádu
-podgrupa řádu  , takže je jedinou Sylowovou
, takže je jedinou Sylowovou 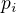 -podgrupou grupy
-podgrupou grupy  .
.
Shrnutím pak skutečně můžeme tvrdit:
Nechť  je prvočíslo, které dělí řád konečné abelovské grupy
je prvočíslo, které dělí řád konečné abelovské grupy  . Grupa
. Grupa  obsahuje právě jednu Sylovowu p-podgrupu, kterou stručně budeme značit
obsahuje právě jednu Sylovowu p-podgrupu, kterou stručně budeme značit 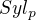 . Tato podgrupa obsahuje všechny p-podgrupy grupy
. Tato podgrupa obsahuje všechny p-podgrupy grupy  a
a  je direktní sumou (bisoučinem, bisúčinem, biproduct) svých
je direktní sumou (bisoučinem, bisúčinem, biproduct) svých 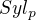 .
.
Offline
#20 17. 12. 2011 21:32
Re: Maximální řád prvku v grupě s k generátory
Dnes som pridal pojem priamej sumy grup
cvicenie 4)
+ esteticke upravy
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 18. 12. 2011 18:29 — Editoval check_drummer (18. 12. 2011 18:55)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
ke cvičení 4) - podle mého je zřejmé, jen je nutné uvažovat i k=0 a definovt, co je  .
.
ke cvičení 5) - implikace "=>" je zřejmá (neformálně): a) každý prvek z G získáme nějakým součtem, b) součet je jednoznačný - v případě, že by průnik v bodu b) obshoval další prvek, je jednoznačnost porušena.
cvičení 5) implikace "<=": existence vyjádření x z definice přímého součtu plyne z a), jednoznačost: platí-li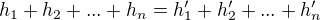 , pak je i
, pak je i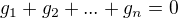 pro
pro  . Pokud jsou všechna
. Pokud jsou všechna 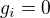 , tvrzení platí. Dále lze (pro spor) předpokládat, že jsou všechna
, tvrzení platí. Dále lze (pro spor) předpokládat, že jsou všechna  . Pro
. Pro  je h inverzí ke
je h inverzí ke  , ovšem tím jsme inverzi k
, ovšem tím jsme inverzi k  vyjádřili pomocí sumy prvků ostatních grup a to je spor s b).
vyjádřili pomocí sumy prvků ostatních grup a to je spor s b).
"Máte úhel beta." "No to nemám."
Offline
#22 18. 12. 2011 18:53 — Editoval vanok (18. 12. 2011 18:53)
Re: Maximální řád prvku v grupě s k generátory
↑ check_drummer:,
Dakujem:
Ano treba uvazovat pochopitelne aj k=0 .... opravil som to
Dnes vecer pridam moj formalny dokaz vety1... ale nasiel si metodu dokazu (to je to najtazsie). :-)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 18. 12. 2011 19:09
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Maximální řád prvku v grupě s k generátory
↑ vanok:
Důkaz 3 mě napadá, ale spíš jen myšlenka - a ani nevím, zda správná: indukcí podle k, kde velikost grupy G je 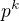 . Pro k=1 zřejmě platí, protože p je prvočíslo, pro obecné k tvoří G celkem p kopií
. Pro k=1 zřejmě platí, protože p je prvočíslo, pro obecné k tvoří G celkem p kopií 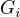 velikosti
velikosti 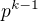 , tj. po aplikaci
, tj. po aplikaci 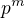 kroků (pro nějaké m) získáme iterací prvku x prvek
kroků (pro nějaké m) získáme iterací prvku x prvek 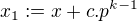 . Je-li c=0 jsme hotovi a není-li uvažujeme další iteraci prvku
. Je-li c=0 jsme hotovi a není-li uvažujeme další iteraci prvku  opět o
opět o 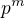 kroků a přesně po p iteracích získáme prvek x (vlastně teď iterujeme v grupě o velikosti p, kde každou
kroků a přesně po p iteracích získáme prvek x (vlastně teď iterujeme v grupě o velikosti p, kde každou 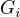 považujeme za jeden prvek a získáme po každé iteraci různou hodnotu c). Je to ale dost neformální vyjádření.
považujeme za jeden prvek a získáme po každé iteraci různou hodnotu c). Je to ale dost neformální vyjádření.
Obrácená implikace je jasná - pro n=a.b obsahují a,b různého prvočíselnéh odělitele a a,b iterujeme b,a kroky a neexistuje násobek b,a obsahující stejného prvočíselného dělitele.
"Máte úhel beta." "No to nemám."
Offline
#24 18. 12. 2011 23:00 — Editoval vanok (19. 12. 2011 00:08)
Re: Maximální řád prvku v grupě s k generátory
Ahoj ↑ check_drummer:,
Ja to vidim jednoduchsie. je p-grupa pre kazde
je p-grupa pre kazde  , kde
, kde  je prvocislo.
je prvocislo.
A reciprocne:
Ak n nema tuto forme existuju dve prvocisla p, q a mame prvok radu p, radu q .....
Myslis ze to staci? to moje riesenie.
Ty ides dalej ako ja, lebo chces riesit vo vseobecnejsom pripade ako je ten problem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 18. 12. 2011 23:34 — Editoval vanok (19. 12. 2011 00:09)
Re: Maximální řád prvku v grupě s k generátory
dnes som pridal uplne riesenie cvicenia 5), co je vlastne dokaz vety 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

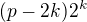 , takže řád toho cyklu bude
, takže řád toho cyklu bude 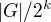 , zkusím se na to ještě podívat, jestli by to nemohlo dávat nějaký odhad toho maxima.
, zkusím se na to ještě podívat, jestli by to nemohlo dávat nějaký odhad toho maxima.


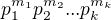 (
(  su rozne )
su rozne ) , rovnostou
, rovnostou 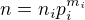
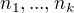 su celkove nesudelitelne ,a tak vdaka Bezout-ovej teoreme existuju
su celkove nesudelitelne ,a tak vdaka Bezout-ovej teoreme existuju  , cele cisla take ze
, cele cisla take ze , co nam da
, co nam da  .
. je rad prvku
je rad prvku  , a tak
, a tak pre kazde
pre kazde 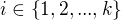 a konecne
a konecne 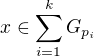
 a
a  .
.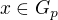 , znamena, ze
, znamena, ze 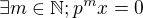
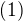
 , znamena, ze
, znamena, ze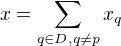 kde
kde 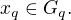
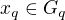 znamena , ze
znamena , ze 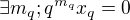
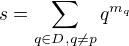
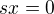
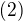 .
. a
a  (Bezout ).
(Bezout ).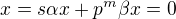
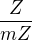 su aditivne
su aditivne kde
kde 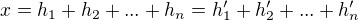 kde
kde 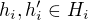 implikuje
implikuje 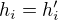 pre kazde
pre kazde 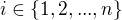


 kde
kde 
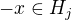 z toho mame
z toho mame 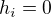 pre kazde
pre kazde 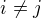 , a konecne
, a konecne 
 kde
kde  a tiez
a tiez 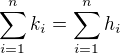 mame
mame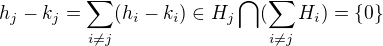
 pre kazde
pre kazde 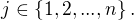
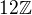 ,
,  ,
,