Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral iracionalni funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 03. 2011 15:19 — Editoval Matik (06. 03. 2011 20:09)
integral iracionalni funkce
zdravim, potreboval bych pomoc s dukazem integralu iracionalni funkce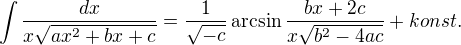 , kde
, kde 
předpoklad  proto bych použil Eulerovu substituci
proto bych použil Eulerovu substituci 
z čehož mi 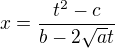
a 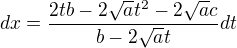
dosadil jsem za  do integrálu
do integrálu 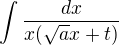 , ten mi vyšel však velmi složitý a nevím si s ním dále rady ... jistě tam asi bude fígl, jak pokračovat v následné úpravě ...
, ten mi vyšel však velmi složitý a nevím si s ním dále rady ... jistě tam asi bude fígl, jak pokračovat v následné úpravě ...
dekuji
Offline
- (téma jako vyřešené označil(a) Matik)
#2 10. 03. 2011 00:06 — Editoval jelena (10. 03. 2011 00:36)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integral iracionalni funkce
Zdravím,
nějak to zapadlo. Pokud jsem nic nepřehledla, tak (snad překlep?) v derivaci (chybí 2. mocnina v jmenovateli)
Po dosazení mi vyšlo:
Po vykrácení by to nebylo moc složité (ještě se podivám, zda jsem něco nepřehledla, protože z takového výsledku bych nedostala arcsin po integrování)
EDIT: teď se mi nezdá už samotný návrh substituce, neb jsem nenašla substituci pro c<0. Upřesní, prosím, jak byla zvolena. Děkuji.
Offline
#3 17. 03. 2011 09:35
Re: integral iracionalni funkce
zdravím,
děkuji moc za příspěvek. Z konzultaí jsem získal jednodušší způsob řešení. Pro zajímavost:
Substituce:
Po úpravách získáme: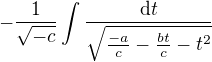
Spodní člen pod odmocninou upravíme rozšířením na čtverec:
Získáme tak: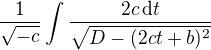 ,
,
kde D je známý diskriminat
Zavedeme opět substituci:
ˇ
Úpravami získáme:
Aplikací vzorce získáme: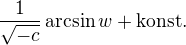
w získáme návraty substitucemi: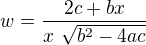
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral iracionalni funkce (TOTO TÉMA JE VYŘEŠENÉ)