Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 03. 2011 23:18
logaritmická rovnice
Ahoj, mám rovnici: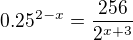
Mohl by mě někdo prosím trochu popostrčit v tom jak pokračovat? (Už nad tím sedím déle než je zdrávo.) Kdybych měl vše dostat na stejný základ nevím jak se vyrovnat s tou 0.25 čili 1/4....
díky
Offline
- (téma jako vyřešené označil(a) r2d2)
#9 16. 03. 2011 08:28 — Editoval miso16211 (16. 03. 2011 14:47)
#10 16. 03. 2011 09:48
Offline

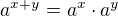 .
.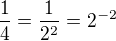
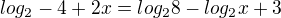
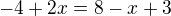
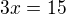
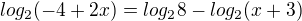 je
je 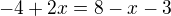
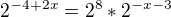
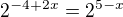
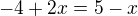
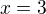
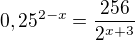
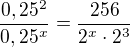
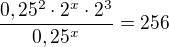
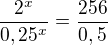
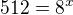
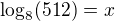
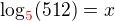 ???
???