Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 03. 2011 22:11
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Wilsonova věta
Wilson's theorem is useless as a primality test in practice, since computing (n − 1)! modulo n for large n is hard, and far easier primality tests are known.
Wilson's theorem
---
Ale ano, určuje (platí tam ekvivalence, viz odkaz), ale vzhledem k náročnosti výpočtu to není vhodné pro hledání prvočísel z množiny nabízených.
Offline
#4 17. 04. 2011 20:36 — Editoval Matej1117 (17. 04. 2011 20:38)
Re: Wilsonova věta
Cisto teoreticky sa da podla Wilsonovej vety na sto percent urcit, ci je dane cislo prvocislo alebo nie. Ale prakticky, keby si chcel overit velke cislo, tak nemas sancu pretoze musis urobit faktorial o 1 mensieho cisla a potom pripocitat este jednotku a ked to videlis danym cislom a ostane ti cele cislo, tak je toto cislo prvocislo. Lenze ak chces overit velke cislo, napriklad 2^100 + 1 tak nemas sancu ani s kalkulackou .. Rovnako mala fermatova veta - je to super sposob ale len teoreticky, prakticky sa s tou mocninou nevybabres ani za mesiac..
Preto som mal taky napad, ze keby sa vo wilsonovej vete (x - 1)! + 1 namiesto tej prvej jednotky dala napr. dvojka, potom by sa muselo pripocitat zrejme nieco ine ako ta jednicka a tym padom by to ulahcilo pocitanie.. a keby sa namiesto jednicky dosadila stovka a namiesto tej druhej jednocky nieco ine tak by to bolo uz tuti fruty.. takyto napad som mal uz davnejsie, aj som sa s tym hrajkal ale mam pocit ze nic take nie je uskutocnitelne .. to je skoda ale rozhodne to nevzdam :)
Offline
#5 17. 04. 2011 20:49 — Editoval FailED (17. 04. 2011 20:49)
Re: Wilsonova věta
↑ Matej1117:
Pozor, Malá Fermatova věta říká, že když je n prvočíslo, potom každé a splňuje 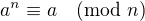 a ne naopak. Fermatův test je jen pravděpodobnostní.
a ne naopak. Fermatův test je jen pravděpodobnostní.
Odkaz
Offline
#7 17. 04. 2011 21:20
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Wilsonova věta
↑ Matej1117:
kolega FailED chce říct, že pokud platí 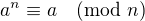 pro všechna a, to ještě nemusí znamenat, že n je prvočíslo. Taková složená čísla se nazývají Carmichaelova čísla (http://en.wikipedia.org/wiki/Carmichael_number)
pro všechna a, to ještě nemusí znamenat, že n je prvočíslo. Taková složená čísla se nazývají Carmichaelova čísla (http://en.wikipedia.org/wiki/Carmichael_number)
Offline