Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 03. 2011 13:06
Offline
#3 25. 03. 2011 13:11 — Editoval OiBobik (25. 03. 2011 13:15)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: konvergence řady
↑ Mr.Pinker:
Poslal bych na to Leibnizovo kritérium.
EDIT: To jsem si špatně rozmyslel, to by nefungovalo, ale každopádně Dirichletovo kritérium by už mělo zabrat (Dirichletovo kritérium třeba zde)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 25. 03. 2011 13:19
Re: konvergence řady
↑ OiBobik:
Někde jsem viděla Leibnitzovo kritérium i v té formě, že ta posloupnost nemusí být klesající, ale stačí být nerostoucí, takže možná ano.
Offline
#5 25. 03. 2011 13:21
Re: konvergence řady
↑ OiBobik:
Co tak tu řadu přímo sečíst :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 25. 03. 2011 13:33 — Editoval OiBobik (25. 03. 2011 13:38)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: konvergence řady
↑ Pavel:
: D jé, a to mě ani nenapadlo si představit.
Ale přece jen - tady to "přímé sečtení", jak ty říkáš, je vlastně "závorkování" některých členů posloupnosti, a to si můžu dovolit udělat jen tehdy, když už vím, že řada konverguje - jinak bych stejnou metodou odvodil, že  , stejně jako
, stejně jako 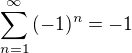 , protože jsem závorkoval řadu, která osciluje. Takže tu konvergenci musím prvně tak či onak stejně vyšetřit. Nebo jsem tě pochopil nějak špatně?
, protože jsem závorkoval řadu, která osciluje. Takže tu konvergenci musím prvně tak či onak stejně vyšetřit. Nebo jsem tě pochopil nějak špatně?
↑ claudia:
Já si taky myslím, že ano (resp. určitě ano - to plyne i přímo z toho Diricheta : )) ), ale běžněji se Leibniz formuluje (asi) pro klesající posloupnosti, tak proč se neodkázat pro jistotu na Dirichleta.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 25. 03. 2011 13:50
Re: konvergence řady
↑ OiBobik:
Zajímavé. Jak nad tím teď přemýšlím, asi neexistuje případ, kde by šlo použít Leibnitzovo krit. a nešlo použít Dirichletovo..? :-)
↑ Mr.Pinker:
Konverguje, lze, např. na řadu kladných členů a řadu záporných členů :-)
Offline
#9 25. 03. 2011 13:59
Re: konvergence řady
↑ OiBobik:
Pokud chci sečíst řadu, tak nic závorkovat nebudu. Stačí určit, čemu se rovná n-tý částečný součet, tzn.
A stačí ukázat, že  . Takto je definován součet nekonečné řady v tzv. Cauchyově smyslu. Uzávorkování se někdy hodí, jen je třeba vědět, kdy jej mohu použít. V tomto případě se však bez něj bez prolbému obejdu. Stejnou metodou lze pak ukázat, že řada
. Takto je definován součet nekonečné řady v tzv. Cauchyově smyslu. Uzávorkování se někdy hodí, jen je třeba vědět, kdy jej mohu použít. V tomto případě se však bez něj bez prolbému obejdu. Stejnou metodou lze pak ukázat, že řada
nekonverguje, popř. osciluje.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 25. 03. 2011 14:01
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: konvergence řady
↑ claudia:
To neexistuje, protože Leibnizovo je vlastně jen speciálním případem Dirichletova: 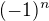 má omezenou posloupnost částečných součtů
má omezenou posloupnost částečných součtů je klesající k nule =>
je klesající k nule =>  je monotónní s limitou 0
je monotónní s limitou 0
Takže vždycky, když mi něco splňuje Leibnize, musí to splňovat i Dirichleta.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 25. 03. 2011 14:08
#12 25. 03. 2011 14:08
Re: konvergence řady
↑ Mr.Pinker:
Konvergentní řadu samozřejmě můžeš rozdělit na dvě divergentní, nicméně nemůžeš takto určovat součet konvergentní řady.
↑ claudia:
to, že neexistuje případ, kde by šlo použít Leibnizovo krit. a nešlo použít Dirichletovo, vyplývá z toho, že Leibnizovo kritérium je spec. případ Dirichletova kritéria.
Jinak taková perlička - Leibniz se píše bez prostředního T, takže ne LeibniTz, ale Leibniz. Marian jako germanista by o tom mohl povykládat ;-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#13 25. 03. 2011 14:11
Re: konvergence řady
↑ claudia:
Musím momentálně pryč. Později se k tomu vrátím a uvedu vzorec pro m-tý částečný součet. Není to však nic složitého, stačí uvážit, jak bude součet vypadat, bude-li m sudé nebo liché.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#14 25. 03. 2011 14:14
#15 25. 03. 2011 14:24 — Editoval Rumburak (25. 03. 2011 14:31)
Re: konvergence řady
↑ Mr.Pinker:
Záleží na tom, zda řada, kterou chceme "rozdělit", konverguje absolutně nebo neabsolutně. Trochu to precisujme.
Uvažujme dvojici rostoucích (nekonečných) posloupností
(1) 
přirozených čísel takových, že
(2) každé přirozené číslo je členem jedné a pouze jedné z posloupností (1).
Mějme konvergentní řadu
(3) 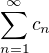 .
.
Otázka zní, zda existuje dvojice posloupností (1) s vlastností (2) a taková, aby obě řady
(4)  .
.
divergovaly. Odpověď je následující:
Pokud řada (3) je absolutně konvergentní, pak ne .
Pokud řada (3) je konvergentní neabsolutně, pak ano.
Offline
#16 25. 03. 2011 14:42
Re: konvergence řady
Ve světle takové preciznosti musím dodat, že jsem tu otázku pochopila tak, jestli se původní zadaná řada dá rozdělit na dvě divergentní.
Že nejde absolutně konvergentní rozložit vyplývá z toho, že  je konvergentní majorantní řada k oběma případně vzniklým?
je konvergentní majorantní řada k oběma případně vzniklým?
A že neabsolutně konvergentní vždy rozložit lze se dá ukázat jak?
Offline
#17 25. 03. 2011 15:34
Re: konvergence řady
↑ claudia:
I.) V podstatě ano: 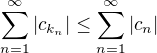 , obdobně
, obdobně 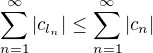 atd.
atd.
II.) Neabsolutně konv. řada se rozdělí na řadu z nezáporných členů a řadu ze záporných členů.
Trochu to rozeberu obecně.
Označíme-li 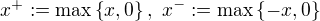 , jsou to nezáporná čísla splňující
, jsou to nezáporná čísla splňující
(1) 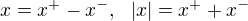 .
.
Sestavíme-li řady
(2) 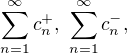 ,
,
potom dle (1) snadno nahlédneme, že pro libovolné přirozené číslo N platí  ,
,  .
.
Odtud plyne:
A. Obě řady (2) konvergují právě tehdy, když řada
(3) 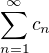
konverguje absolutně.
B. Konverguje-li z řad (2) právě jedna, potom řada (3) diverguje .
C. Pokud obě řady (2) divergují, pak řada (3) může konvergovat, ale ne absolutně.
Zpětně vzato: Jestliže řada (3) konverguje neabsolutně, znamená to, že máme případ C.
Offline
#18 25. 03. 2011 16:48
Re: konvergence řady
↑ claudia:
Nechť  je sudé, tj.
je sudé, tj. 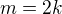 ,
, 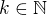 . Pak
. Pak
Nechť  je liché větší než 1, tj.
je liché větší než 1, tj. 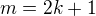 ,
, 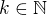 . Pak
. Pak
Odtud je vidět, že  , tzn.
, tzn. 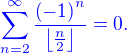
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#19 25. 03. 2011 21:16
Re: konvergence řady
↑ Pavel:
Děkuji, asi jsi to napsal výstižněji, než by se podařilo mně :-) Přesto bych si dovolila tvrdit, že OiBobikovo řešení s použitím Dir. krit. by bylo stručnější :-)
↑ Rumburak:
To je pěkný důkaz, děkuji.
Offline
![kopírovat do textarea $\sum \nolimits_{n=1}^{\infty}\frac{(-1)^n}{[\frac{n}{2}]}$](/mathtex/73/73b1f18077ce1a03807f250f37fef836.gif)
![kopírovat do textarea $[\frac{n}{2}]$](/mathtex/57/570aee2b38b6704e5e4995c43e88a2db.gif) ...má bejt celá část
...má bejt celá část
