Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Trigonometric equation (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 03. 2011 03:40
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Trigonometric equation
Let  . Where
. Where 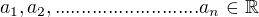 .
.
If 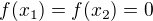 . Then
. Then 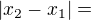
Offline
- (téma jako vyřešené označil(a) byk7)
#2 28. 03. 2011 10:36 — Editoval musixx (28. 03. 2011 11:05)
Re: Trigonometric equation
Firstly, we must realize that  is not constant. But
is not constant. But 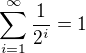 , so therefore any finite sum
, so therefore any finite sum 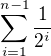 is smaller than 1. For sure, there is such
is smaller than 1. For sure, there is such 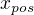 that
that  . Since
. Since  , then also
, then also  for any sequence
for any sequence 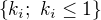 , so specially for a sequence
, so specially for a sequence  . Therefore
. Therefore  . Analogically, we can show that there exists
. Analogically, we can show that there exists 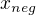 such that
such that  . So our function
. So our function  is not a constant one. EDIT: A constant function would degenerate the following...
is not a constant one. EDIT: A constant function would degenerate the following...
---------------
Futher (an extension via the induction): a linear combination
is equal to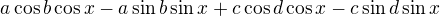 , so also to
, so also to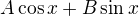 , so also to
, so also to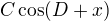 (for suitable constants)
(for suitable constants)
mentioned e.g. here (in Czech), so your whole function  is nothing more than
is nothing more than  for suitable constants
for suitable constants  and
and  , where
, where  is nonzero because of the previous paragraph. Therefore your
is nonzero because of the previous paragraph. Therefore your 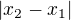 is an integral multiple of
is an integral multiple of  , since there is -- in the end -- nothing more than one single cosinus.
, since there is -- in the end -- nothing more than one single cosinus.
---------------
A remark: We used strongly a fact how  was used in all the arguments. A general counter-example:
was used in all the arguments. A general counter-example: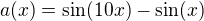
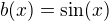 .
.
Minimal periods: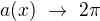
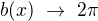
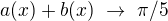
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Trigonometric equation (TOTO TÉMA JE VYŘEŠENÉ)