Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » první a druhá derivace , extrémy (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 03. 2011 12:36
první a druhá derivace , extrémy
Prosím Vás o pomoc.... dostal jsem za úkol vypracovat 2 příklady a u každého vypočítat těchto 9 bodů... částečně jsem dal dohromady ten první příklad, ale ten druhý..., jak je tam ten zlomek, tak na to prostě nemam... Děkuju Vám moc za pomoc.. :)
1. D (f) – limity v krajních bodech definičního oboru.
2. První a druhá derivace.
3. lokální extrémy.
4. (monotonost funkce) – rostoucí a klesající.
5. Inflexní body.
6. Konkálnost a Konvexnost.
7. Průsečíky funkce s osou ( odhad)
8. asymptoty funkce, (pokud budou).
9. graf funkce.
10. tabulka funkčních hodnot.
První příklad :
y=x na třetí, mínus tři x na druhou, mínus devět x.
Druhý příklad:
y=jedna lomeno x, plus x.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 27. 03. 2011 13:44
Re: první a druhá derivace , extrémy
↑ jardas:
Moc Vás prosím o pomoc.... mám to mít do zítra hotový a nevím si s tím rady... jsem zoufalej... Když mi pomůžete, já Vám to nějak zaplatim... Prosím... mam matiku mezi čtyřkou a pětkou..., když to přinesu do zítra spávně vypočítaný, dostanu dobrou známku a nebudu muset dělat reparát...Prosím..
Offline
#3 27. 03. 2011 13:48
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: první a druhá derivace , extrémy
Hezké odpoledne přeji.
Funkce je tedy definovaná jako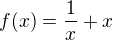 ,
,
čtu to dobře? Jestli ano, tak můžeme jít bod po bodu.
1. Do definičního oboru asi bude patřit vše až na nulu, je to tak?
2. Derivaci uděláme jako derivaci součtu. , to je snad jasné,
, to je snad jasné, 
Navážete?
Offline
#4 27. 03. 2011 13:54
Re: první a druhá derivace , extrémy
↑ halogan:
Jak děláte ty obrázky s výpočty ? já bych navázal, ale nevim, jak se dělají...
Offline
#5 27. 03. 2011 13:57
Re: první a druhá derivace , extrémy
↑ jardas: základy texu (to jsou ty "obrázky s výpočty"): http://forum.matweb.cz/viewtopic.php?id=224
Offline
#7 27. 03. 2011 14:08
Re: první a druhá derivace , extrémy
↑ jardas: pokud chceš psát bez texu, dodržuj alespoň základní zásady. jinak nikdo normální nebude mít chuť to po tobě luštit
Offline
#9 27. 03. 2011 14:18
Re: první a druhá derivace , extrémy
↑ halogan:
děkuju.., byl by jste hodný, kdyby jste to se mnou dělal bod po bodu...
1. podle mě tam můžou být všechna až na nulu, protože nulou se dělit nesmí..
2.  a druhá derivace je
a druhá derivace je 
je to tak ?
Offline
#11 27. 03. 2011 15:07
Re: první a druhá derivace , extrémy
Možná kolegu zmátlo:
halogan napsal(a):
Zřejmě bylo myšleno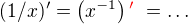
Offline
#12 27. 03. 2011 15:08
Re: první a druhá derivace , extrémy
↑ halogan:
no, snad je to správně.. budu Vám důvěřovat a ta druhá derivace tedy je...
je to tak ?
Offline
#13 27. 03. 2011 15:10
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: první a druhá derivace , extrémy
↑ claudia:
Samozřejmě, překlepl jsem se a nevytexovala se derivace.
↑ jardas:
Nedůvěřujte mně, už jednou jsem se dneska překlepl :-)
Psal bych raději 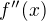 , protože přeci jen jde o druhou derivaci.
, protože přeci jen jde o druhou derivaci.
Máme tedy druhý bod hotov. Co vám nejde u toho třetího?
Offline
#14 27. 03. 2011 15:14 — Editoval claudia (27. 03. 2011 15:15)
Re: první a druhá derivace , extrémy
Tip: Má-li funkce v bodě a lokální extrém, pak první derivace funkce v bodě a neexistuje nebo 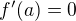 . Kde první derivace neexistuje? Kde je nulová? Který z těch bodů může být extrém? Který nemůže? Proč? :-)
. Kde první derivace neexistuje? Kde je nulová? Který z těch bodů může být extrém? Který nemůže? Proč? :-)
Offline
#15 27. 03. 2011 15:15
#16 27. 03. 2011 15:18 — Editoval claudia (27. 03. 2011 15:19)
Re: první a druhá derivace , extrémy
Možná je to tak. Ale není to v tuto chvíli ještě jasné, protože ne v každém bodě, kde je první derivace nulová, musí mít funkce lokální extrém. Je tedy třeba nějakou metodou ověřit, že opravdu má. (Např. že na jednu stranu od toho bodu je funkce klesající, na druhou rostoucí, nebo za použití 2. derivace).
Z toho důvodu já obvykle vyšetřuji monotonii dříve než lokální extrémy.
Offline
#17 27. 03. 2011 15:22
Re: první a druhá derivace , extrémy
↑ claudia:
jinak řečeno... potřebuju najít body, které jsou podezřelé z extrémů, pokud tam nějaký jsou... je to tak ?
Offline
#18 27. 03. 2011 15:24
#19 27. 03. 2011 15:25
Re: první a druhá derivace , extrémy
jardas napsal(a):
↑ claudia:
jinak řečeno... potřebuju najít body, které jsou podezřelé z extrémů, pokud tam nějaký jsou... je to tak ?
Ano, body podezřelé z extrémů jsou právě ty, kde je první derivace nulová nebo neexistuje.
Offline
#20 27. 03. 2011 15:26
Re: první a druhá derivace , extrémy
jardas napsal(a):
↑ claudia:
Takže teď počítám toto :
je to tak ?
Podle toho, co počítáš :-) Pokud se snažíš vyšetřit monotonii, tak tudy cesta vede :-)
Offline
#21 27. 03. 2011 15:31
Re: první a druhá derivace , extrémy
↑ claudia:
To mě napadlo taky, když tyhle 2 příklady u kterých mam udělat 9 bodů počítam už týden... :D a furt mi to nešlo.. poslední možnost, která mě napadla byla, že se obrátim na matematické forum a že to za pomoci druhých dam nějak dohromady...
Tak kudy ta cesta vede ? :)
Offline
#22 27. 03. 2011 15:36
Re: první a druhá derivace , extrémy
↑ claudia:
já myslel, že u monotomie se dosazuje první derivace a zkouší se v jakém intervalu je to menší a v jakém větší než nula..
Offline
#23 27. 03. 2011 15:36 — Editoval claudia (27. 03. 2011 15:41)
Re: první a druhá derivace , extrémy
Správně to píšeš, řešením těch nerovnic. (Náhodou ti to jde docela pěkně, na to, že píšeš, že z matiky propadáš. Mnozí jsou tady sebevědomější s horšími znalostmi :-)
Víme, že pokud je první derivace v bodě kladná, pak je v tom bodě funkce rostoucí. Podíváme se tedy, kde je kladná:
Z toho můžeme usoudit, že funkce je rostoucí v intervalech (vč. hraničních bodů): ![kopírovat do textarea $\(-\infty,-1\]$](/mathtex/86/86d83052ff2ea0f16251ca2f4b123441.gif) a (nikoli sjednoceno)
a (nikoli sjednoceno)  .
.
Zkus tu druhou stejně.
Offline
#24 27. 03. 2011 15:47
#25 27. 03. 2011 15:51 — Editoval claudia (27. 03. 2011 15:53)
Re: první a druhá derivace , extrémy
↑ jardas:
Ne. Jaké úpravy děláš v jednotlivých řádcích? Mimochodem, absolutní hodnota ničeho nikdy není záporná. Ten poslední krok je vyloženě ošklivý.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » první a druhá derivace , extrémy (TOTO TÉMA JE VYŘEŠENÉ)
 ,
,






