Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 03. 2011 15:28
Re: Vektory,lineární závislost
Nejsnazší by mi přišlo napsat si je do matice a využít poznatku, že pokud budou závislé, pak bude determinant nulový. Stačí tak?
Offline
#3 27. 03. 2011 15:46
- Wolframius

- Příspěvky: 27
- Reputace: 0
Re: Vektory,lineární závislost
My sme sa učili riešiť to cez maticu ako píše claudia, pričom pre LZ platí, že počer nenulových riadkov matice sa nerovná počtu neznámich.
po prerátaní by ti mala vísť matica:
0 a2-4 0
0 0 -1
1 2 1
(3 neznáme -> aspoň jeden musí byť nulový aby platila LZ)
Majú byť LZ a teda 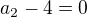 potom
potom 
Offline
#4 27. 03. 2011 16:02 — Editoval claudia (27. 03. 2011 16:02)
#5 27. 03. 2011 16:10 — Editoval Wolframius (27. 03. 2011 16:12)
- Wolframius

- Příspěvky: 27
- Reputace: 0
Re: Vektory,lineární závislost
↑ claudia:
Mohol som písať
k l m
0 a2-4 0 | 0
0 0 -1 | 0
1 2 1 | 0
kde k,l,m sú tie neznáme
Offline
#7 27. 03. 2011 16:15
Re: Vektory,lineární závislost
Je možné najít inspiraci i ve vedlejším tématu :-)
http://forum.matweb.cz/viewtopic.php?id=28836
Ale postup s determinantem je přesto snazší, znáš-li příslušnou teorii.
Offline
