Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 03. 2011 13:26
- Dana1
- Host
Re: absolutna hodnota v absolutnej hodnote
↑ ivec:
Absolútna hodnota niečoho je väčšia ako 3, keď to niečo je buď väčšie ako 3 alebo menšie ako -3.
V Tvojom prípade I.  alebo II.
alebo II. 
#3 28. 03. 2011 13:28 — Editoval musixx (28. 03. 2011 13:47)
Re: absolutna hodnota v absolutnej hodnote
↑ ivec: Ne. Není to ale žádná věda...
Navíc ↑ Dana1: už nabídla alternativní řešení, které funguje v této konkrétní situaci.
Ale podívejme se na to obecněji. Jistě bude třeba rozlišit, jak funkce vypadá na intervalech  a
a  . Na prvním je to
. Na prvním je to  , na druhém je to
, na druhém je to  .
.
Pro první výsledek  , tedy na intervalu
, tedy na intervalu  se ještě musíme ptát, co s funkcí "udělá" nulový bod
se ještě musíme ptát, co s funkcí "udělá" nulový bod  . Zřejmě tedy je třeba vyšetřovat chování zvlášť pro intervaly
. Zřejmě tedy je třeba vyšetřovat chování zvlášť pro intervaly  a
a  , protože "nový" nulový bod
, protože "nový" nulový bod  padl do intervalu
padl do intervalu  .
.
Pro druhý výsledek  , tedy na intervalu
, tedy na intervalu  se ještě musíme ptát, co s funkcí "udělá" nulový bod
se ještě musíme ptát, co s funkcí "udělá" nulový bod 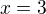 . Zřejmě tedy je třeba vyšetřovat chování zvlášť pro intervaly
. Zřejmě tedy je třeba vyšetřovat chování zvlášť pro intervaly  a
a  , protože "nový" nulový bod
, protože "nový" nulový bod  padl do intervalu
padl do intervalu  .
.
----------------------------
Poznámka: Šlo-li by třeba o funkci  , pak bude situace malinko jiná. Uvádím jako příklad, že ne vždy se musí funkce "rozpadnou na stejný počet částí".
, pak bude situace malinko jiná. Uvádím jako příklad, že ne vždy se musí funkce "rozpadnou na stejný počet částí".
Opět začínám od nejvnitřnějších absolutních hodnot a ptám se proto, jak funkce vypadá na intervalech  a
a  . Na prvním je to
. Na prvním je to  , na druhém
, na druhém  .
.
Ovšem potenciální nulový bod pro první interval, tedy bod 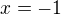 leží mimo interval
leží mimo interval  , proto funkce tam nikdy nemůže vypadat jako
, proto funkce tam nikdy nemůže vypadat jako  , tedy je rovna
, tedy je rovna  na celém
na celém  .
.
Analogicky pro interval  , kde je pro změnu potenciální nulový bod
, kde je pro změnu potenciální nulový bod 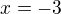 mimo, a proto tam funkce vždy vypadá jako
mimo, a proto tam funkce vždy vypadá jako 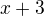 .
.
Offline
#4 28. 03. 2011 13:35 — Editoval Rumburak (28. 03. 2011 14:02)
Re: absolutna hodnota v absolutnej hodnote
Takovou úlohu lze řešit substitucí - ve dvou etapách:
1. Položíme  a vyřešíme soustavu nerovnic
a vyřešíme soustavu nerovnic  , množinu všech jejích řešení označíme A.
, množinu všech jejích řešení označíme A.
2. Dále budeme hledat množinu B všech x , pro která je  , což opět povede na řešení nějakých nerovnic.
, což opět povede na řešení nějakých nerovnic.
Množina B bude zároveň množinou všech řešení původní nerovnice  .
.
POZNÁMKA. Obdobně postupovala i Dana (viz ↑ Dana1:), zvolila však (de facto) substituci  .
.
Kolega ↑ musixx: ukázal postup zcela jiný - je dobré rozumět oběma.
Offline
#5 28. 03. 2011 14:16
Re: absolutna hodnota v absolutnej hodnote
panove Musixxove je prilis velkolepe na to aby som na nieco take prisiel sam :-D, a tie substitucie mi to vlastne aj vyriesili, teda dakujem za napad, sice mi vysli len dve z troch vyslednych intervalov ale aspon nieco;) a cez tabulku s nulovymi bodmi sa nieco take vyriesit neda naraz bez substitucii?
Offline
#6 28. 03. 2011 14:36 — Editoval musixx (28. 03. 2011 14:41)
Re: absolutna hodnota v absolutnej hodnote
ivec napsal(a):
... cez tabulku s nulovymi bodmi sa nieco take vyriesit neda naraz bez substitucii?
Dá, a jde o to mé
ivec napsal(a):
panove Musixxove je prilis velkolepe...
řešení. Vlastně chybí jen krůček od toho, co jsem už spočítal.
Tedy máme nulové body -7, -2 a 3 (tedy je-li x rovno některému z těchto čísel, pak některá absolutní hodnota je nulová: takto je třeba pojem nulového bodu vnímat).
Offline
#7 28. 03. 2011 15:22
Re: absolutna hodnota v absolutnej hodnote
↑ ivec:
Ta metoda nulových bodů vychází přímo z definice absolutní hodnoty.
Jak vime, definice absolutní hodnoty má dvě větve :
1.  ,
,
2.  .
.
Proto, chceme-li se např. ve funkčním výrazu  zbavit abs. hodnoty, je jednou z možností bezprostředně použít předchozí definici.
zbavit abs. hodnoty, je jednou z možností bezprostředně použít předchozí definici.
Dostaneme pak
1' .  ,
,
2' .  ,
,
tím se úloha "vyjádřit |f(x)| bez použití absolutní hodnoty" rozvětví na dvě části.
Ve středoškolských úlohách se na místě funkce f zpravidla vyskytuje taková funkce, jejímž grafem je nějaká souvislá křivka.
Pak jsou s hledika nalezení hranice mezi kroky 1' , 2' důležité průsečíky tohoto grafu s osou x, což vede k rovnici f(x) = 0 - odtud
máme "metodu nulových bodů" . Není to tedy nějaká mechanická metoda, ale metoda, která má své odůvodnění. Na základě
porozumění konkretní úloze mohu rozhodnout, zda a jakým způsobem mám tuto metodu použít.
Offline
#10 06. 07. 2011 20:04
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: absolutna hodnota v absolutnej hodnote
stači si načrtnuť graf funkcii  a to tak že načrtneš
a to tak že načrtneš 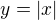 a potom posunieš graf smerom doľava
a potom posunieš graf smerom doľava
potom posunieš dole o 5 dieliky a pak určiš bodz v ktorych pretina tento graf priamku y = 3 a je to.
Rovnice a nulove body som nikdz nechapal, až som si nato vymyslel svoj štýl ako to riešiť, keď niečo nechapeš môžeš isť na online pomoc a napíš mi správu, čau
Offline
#11 06. 07. 2011 21:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: absolutna hodnota v absolutnej hodnote
Zdravím vás, téma už je dost nepřehledné, ale snad se zorientujeme:
↑ laylitta:
pokud je to řešení nerovnic na jednotlivých intervalech, potom bys měla vytvořit průniky mezi řešením nerovnice na každém intervalu a podmínkou pro interval.
Za použití tabulky od kolegy ↑ musixx: (děkuji velice, omlouvám se, že pokazím celou estetiku) dořeš prosím 
--------------------------------------------------------------------------
↑ miso16211:
Děkuji za doporučení. Tvůj návrh lze použit pro zakreslení grafického řešení  , ovšem pro úlohu ze zadání
, ovšem pro úlohu ze zadání  ještě je třeba použit další absolutní hodnotu a obrátit špíčku V nad osu x, tedy místo
ještě je třeba použit další absolutní hodnotu a obrátit špíčku V nad osu x, tedy místo  budeme mít
budeme mít  . Zadej to prosím do WolframAlpha, pokud máš chvilku. Je to tak? Děkuji.
. Zadej to prosím do WolframAlpha, pokud máš chvilku. Je to tak? Děkuji.
OT: nemyslím, že by byla nějaká námitka proti nápadu na online pomoc kolegy mikee, ale propaguj to prosím jinou formou, než nabízením v konkrétním matematickém tématu. Na OT prosím nereagovat v tomto tématu. Děkuji.
Offline
#12 07. 07. 2011 14:20
#13 07. 07. 2011 15:03 — Editoval musixx (07. 07. 2011 15:18)
Re: absolutna hodnota v absolutnej hodnote
↑ miso16211: To jsi se asi nechal příliš unést nějakými konkrétními příklady. Co třeba
nebo
nebo snad .
.
EDIT: Rozumím tomu, jak to chceš postupně konstruovat, a nic proti tomu nemám. Ale jak budeš bez výpočtů sčítat v f(x), případně "otáčet nad osu x" graf funkce ||x|-2|-1 v případě mého druhého příkladu g(x)?
Offline
#14 08. 07. 2011 12:53 — Editoval pepa999 (08. 07. 2011 13:07)
Re: absolutna hodnota v absolutnej hodnote
↑ ivec:
Pokud tě zajímají čistě nulové body, tak položíš vnitřek té "hlavní" absolutní hodnoty roven nule.... a upravuješ
a upravuješ


(absolutní hodnota rozdílu dvou čísel se rovná vzdálenosti jejich obrazů na číselné ose a nebo ještě jinak, tuto poučku ani nemusíš znát. Prostě, když dosadíš za x = -2+-5, tak vnitřek absolutní hodnoty bude +5 respektive -5(-dvojky se pokrátí), takže absolutní hodnota bude 5. Pro žádný jiný čísla už +-5 uvnitř absolutní hodnoty nedostaneš(tedy ani 5 jako výsledek absolutní hodnoty), protože lineární funkce y=ax+b je prostá.)
Offline
#15 11. 03. 2012 08:50
- rebirth_boy

- Příspěvky: 33
- Reputace: 0
Re: absolutna hodnota v absolutnej hodnote
Zdravim forum, nechcem zakladat novu temu tak snad nevadi ak vytiahnem staru. Mam totiz problem s absolutnou hodnotou v absolutnej hodnote a akosi si to neviem vysvetlit, obycajnym absolutnym hodnotam rozumiem ale vnorenym nie, resp. ich grafu.
toto je normalna absolutna hodnota, tomu rozumiem...
aj tomuto rozumiem, absolutna hodnota sa posunie o stupen nizsie...
toto mi uz nieje jasne, pretoze si neviem vysvetlit tie "vlnovky"
Offline
#16 11. 03. 2012 11:22
Re: absolutna hodnota v absolutnej hodnote
Pro doplnění uvádím další možnost rěšení původní nerovnice. Je zřejmé, že pro všechna reálná  jsou obě strany nerovnice nezáporné. Z tohoto poznatku plyne, že umocnění na druhou je pro tuto nerovnici ekvivalentní úprava.
jsou obě strany nerovnice nezáporné. Z tohoto poznatku plyne, že umocnění na druhou je pro tuto nerovnici ekvivalentní úprava.


1) 


![kopírovat do textarea $K_{1}=[(-\infty;-10)\cup (-4;\infty)]\cap (-\infty;-2\rangle$](/mathtex/e6/e61e3ef9c8562ec3950836e44afd2ed5.gif)

2) 


![kopírovat do textarea $K_{2}=[(-\infty;0)\cup (6;\infty)]\cap (-2;\infty)$](/mathtex/c1/c119fbd9069cde62f3214f6fd16f6a39.gif)



Offline
#17 11. 03. 2012 12:30
Re: absolutna hodnota v absolutnej hodnote
poznamka
pozri sa aj sem
http://forum.matweb.cz/viewtopic.php?pid=267176#p267176
Mozno sa ti to bude zdat ako reklama na tabulkovu metodu.
Ale skutocne, vdaka nej sa vsetko jednoduchsie riesi.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 11. 03. 2012 14:08
- rebirth_boy

- Příspěvky: 33
- Reputace: 0
Re: absolutna hodnota v absolutnej hodnote
ok, diki:) myslim ze tomu uz trocha rozumiem
Offline


