Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 03. 2011 21:11
Re: rovnice tečen ke křivce
Umis tu funkci zderivovat? pomoci derivace najdes smernici tecny.
tecny je tvaru:  ,
,  se bude obecne rovnat prvni derivaci te funkce. Q zjistis, pokud za x a y dosadis do rovnice bod M a vyjde ti pravdepodobne kvadraticka rovnice. Ta bude muset mit diskriminant nulovy, z toho urcis q.
se bude obecne rovnat prvni derivaci te funkce. Q zjistis, pokud za x a y dosadis do rovnice bod M a vyjde ti pravdepodobne kvadraticka rovnice. Ta bude muset mit diskriminant nulovy, z toho urcis q.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#4 29. 03. 2011 23:01 — Editoval Dana1 (29. 03. 2011 23:48)
- Dana1
- Host
Re: rovnice tečen ke křivce
↑ Cast:
Graf funkcie: Odkaz
Keď poznáš bod dotyku, tak 1. derivácia funkcie, ku ktorej grafu robíš dotyčnicu v bode dotyku je smernica dotyčnice.
Ale Ty bod dotyku nepoznáš.
Dotyčnice viem zistiť, ale smernicu neurčujem pomocou derivácie...
Rovnica dotyčnice:  obsahuje bod
obsahuje bod ![kopírovat do textarea $M[3;0]$](/mathtex/ab/ab1f6e9bef159e4f725f3e27b8a0aca7.gif) . Platí teda
. Platí teda 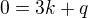 , z toho
, z toho 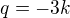 . Potom rovnica dotyčnice je
. Potom rovnica dotyčnice je  .
.
Dotyčnica má mať s krivkou spoločný jediný bod, hľadám teda prienik krivky a dotyčnice (dosadím za y do rovnice krivky y priamky):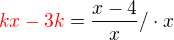 , dostanem kvadratickú rovnicu
, dostanem kvadratickú rovnicu 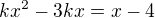 , upravím na tvar
, upravím na tvar 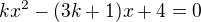 .
.
Od tejto rovnice chcem, aby mala len jediné riešenie (spoločný má byť iba jeden bod - bod dotyku), teda jej diskriminant sa má rovnať 0.
Zapíšem 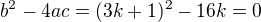 . Tejto rovnici vyhovujú dve hodnoty koeficientu k, ktoré zodpovedajú dvom dotyčniciam vedeným z bodu M.
. Tejto rovnici vyhovujú dve hodnoty koeficientu k, ktoré zodpovedajú dvom dotyčniciam vedeným z bodu M. . Rovnice dotyčníc budú podľa toho
. Rovnice dotyčníc budú podľa toho 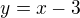 a
a 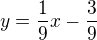 , pričom druhá rovnica sa dá ešte upraviť.
, pričom druhá rovnica sa dá ešte upraviť.
#7 28. 05. 2017 11:02
- misaH
- Příspěvky: 13460
Re: rovnice tečen ke křivce
↑ thatsmis:
Ahoj.
Prečítaj si, čo píše Phate.
Offline

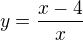 K výpočtu směrnice užijte derivaci.
K výpočtu směrnice užijte derivaci.