Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 04. 2011 11:26 — Editoval Baktor (04. 04. 2011 11:29)
Integrál pomocí mocninných řad
Zdravím, potřebuji prosím poradit co nejrychleji jak vypočítat tento příklad:
Vypočítejte s přesností na tři desetinná místa integrál:
http://www.wolframalpha.com/input/?i=in … rom+0+to+1
funkci rozložíte do mocninné řady. Prověřte platnost podmínek, které tento postup
umožňují.
Někdo už sem stejný příklad dával nedávno, ale ta rada mi moc nepomohla. Zkoušel jsem už všechno, pořád mi to nevychází, potřeboval bych přesný postup a ověření těch podmínek, moc byste mi pomohli. Děkuji mockrát!
Offline
#2 04. 04. 2011 12:01
Re: Integrál pomocí mocninných řad
↑ Baktor:
Čemu nerozumíš?
rozvoj fce cos(x) lze najít na mnoha místech (např.Zde)
Uděláš rozvoj cos(x) odečteš 1, podělíš x^2 a dostaneš úplně jednoduchou mocninnou řadu. Tu zintegruješ člen po členu a vezmeš tolik členů, aby výsledek byl přesnější než požadovaná přesnost.
Platnost podmínek si už udělej.
Offline
#4 04. 04. 2011 16:51
Re: Integrál pomocí mocninných řad
↑ Bibo:
K tomu, abychom mohli funkční řadu integrovat člen po členu, samotná její konvergence nestačí .
Avšak velmi názorně platí:
Konverguje-li řada  spojitých funkcí na uzavřeném intervalu [a, b] stejnoměrně, potom
spojitých funkcí na uzavřeném intervalu [a, b] stejnoměrně, potom
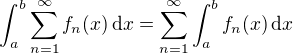 .
.
Offline
