Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kvadratická rce s imaginárními koeficienty (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 04. 2011 18:42
Kvadratická rce s imaginárními koeficienty
Mám řešit rovnici x^2 - (4-i)x +9-7i=0
Dostal jsem se k tomu, že D=-21+20i a absolutní hodnota D je 29. Po dosazení do vzorce mi ale vycházej strašný čísla. Poradíte prosím co dělám špatně?
Offline
- (téma jako vyřešené označil(a) hradecek)
#5 14. 04. 2011 19:49
Re: Kvadratická rce s imaginárními koeficienty
↑ vajcoj:
ALe ono to není tak složitý. Člen s  musí být ten člen
musí být ten člen  , takže si to číslo u
, takže si to číslo u  vydělíš dvěma a to co ti zůstane rozložíš na součin. U školních příkladů se ten součin dá udělat jen několika málo způsoby. Např. tady po vydělení dvěma mám
vydělíš dvěma a to co ti zůstane rozložíš na součin. U školních příkladů se ten součin dá udělat jen několika málo způsoby. Např. tady po vydělení dvěma mám  a to lze jen
a to lze jen  nebo
nebo 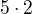 . A dvě možnosti už prozkoušíš.
. A dvě možnosti už prozkoušíš.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kvadratická rce s imaginárními koeficienty (TOTO TÉMA JE VYŘEŠENÉ)

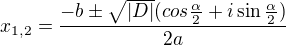
 je argument goniometrického tvaru
je argument goniometrického tvaru 

