Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 04. 2011 19:55
- Dana1
- Host
Re: rovnice
Nechýba Ti tam niekde ešte 1 m? A pokiaľ si prišiel? V čom sa Ti nedarí?
#4 18. 04. 2011 20:17 — Editoval Dana1 (18. 04. 2011 20:21)
- Dana1
- Host
Re: rovnice
↑ jasir:
3+5 je totiž 8, prečo by niekto nechával čitateľ zlomku v tejto podobe?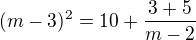
Okrem toho to potom vyzerá na rovnicu tretieho stupňa, čo na ZŠ neberú...

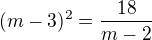
 a pokud to dáme vyřešit wolframu, poví nám, že
a pokud to dáme vyřešit wolframu, poví nám, že 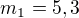 cca a dále dva kořeny
cca a dále dva kořeny