Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 20. 04. 2011 01:04
Re: Báze ortogonálního doplňku
 je zrovna řešení, které tě spíš nezajímá - je zapotřebí najít nějaké netriviální řešení. Jelikož má celý prostor polynomů max. 2. stupně dimensi 3 a
je zrovna řešení, které tě spíš nezajímá - je zapotřebí najít nějaké netriviální řešení. Jelikož má celý prostor polynomů max. 2. stupně dimensi 3 a  má dimensi 2, bude mít
má dimensi 2, bude mít  dimensi 1, tedy stačí najít jedno netriviální řešení uvedené soustavy a to už bude bází
dimensi 1, tedy stačí najít jedno netriviální řešení uvedené soustavy a to už bude bází  . Možná pomůže dosadit něco jako
. Možná pomůže dosadit něco jako  a rozepsat skalární součiny podle jejich definice - dostane se z toho soustava běžných lineárních rovnic.
a rozepsat skalární součiny podle jejich definice - dostane se z toho soustava běžných lineárních rovnic.
Jinou možností je vzít nějaký polynom mimo  , spočítat jeho kolmý průmět na
, spočítat jeho kolmý průmět na  a ten pak od něj odečíst - opět dostaneme bázový vektor.
a ten pak od něj odečíst - opět dostaneme bázový vektor.
Offline



 .
.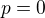 tak to bude platit, co z toho plyne?
tak to bude platit, co z toho plyne?




