Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 04. 2011 13:03
Re: obsah stvorca
↑ jozotom:
Návod:
A = [0, y] , B = [x, 0] , C = [13, 8] nechť jsou ony tři vrcholy čtverce dle zadání. Klíčem k řešení bude nalézt bod B = [x, 0],
tedy nezámé číslo x. O vektorech A-B, C-B víme toto:
- mají stejnou velikost,
- jsou na sebe kolmé.
Z těchto informací sestavíme soustavu rovnic pro x, y.
Offline
#3 22. 04. 2011 13:17
Re: obsah stvorca
No skusim...
Ak su vektory kolme to znamena, ze ich skalarny sucin je rovny 0.
Takze...
AB=(x-0,0-y)
BC=(13-x,8)
___________________________
a.b=0
x.(13-x)+8.(-y)=0 -13x+y=0................. Kedze B(x,0) takze y=0
-13x+y=0................. Kedze B(x,0) takze y=0 -13x+0=0
-13x+0=0 -13x=0
-13x=0
x.(x-13)=0
x=0
x=13
Postupoval som dobre ??
0,9999999...=1
Offline
#4 22. 04. 2011 13:46 — Editoval Rumburak (22. 04. 2011 14:07)
Re: obsah stvorca
Rovnice
(1) 
je ještě správně, pak nastává chyba: symbolem y jsme označili neznámou y-ovou souřadnici bodu A, (ne bodu B) ,
proto z pdmínky B =[x, 0] neplyne, že by mělo být y = 0.
To, co je potřeba místo toho udělat , je vyjádřit další rovnicí tu informaci, že čtverec má všechny strany stejně dlouhé,
speciálně pak strany BA, BC.
Offline
#6 22. 04. 2011 14:38 — Editoval Rumburak (22. 04. 2011 14:41)
Re: obsah stvorca
Ta délka strany BC měla vyjít 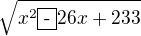 - chyba při umocňování dvojčlenu.
- chyba při umocňování dvojčlenu.
Máme tedy celkem dvě rovnice  ,
, 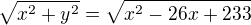 ,
,
které tvoří soustavu o dvou neznámých. Tu vyřešíme - staší zjistit jen jednu neznámou.
Budeme-li znát x, vypočteme obsah čtverce pomocí délky strany,
budeme-li znát y, vypočteme obsah čtverce pomocí délky úhlopříčky.
Offline
#7 22. 04. 2011 14:51 — Editoval Cheop (22. 04. 2011 14:54)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: obsah stvorca
↑ Rumburak:
Pořád si nemohu pomoci:
Ta první rovnice má být: (už to počítám po x-té)
Obsah čtverce 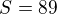
Nikdo není dokonalý
Offline
#8 22. 04. 2011 14:57 — Editoval jozotom (22. 04. 2011 15:11)
Re: obsah stvorca
Máš pravdu urobil som hore chybu...
ma byt..
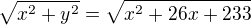
Neviem vypocitat tuto sustavu.. Vzdy mi vychadza nieco zlozite ako ste postupovali ?? Inak vysledok mate dobry
Postupujem asi takto... upravim to

___________________________
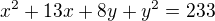
A dalej uz neviem ako prist na vysledok
0,9999999...=1
Offline
#9 22. 04. 2011 15:54 — Editoval Rumburak (22. 04. 2011 16:04)
Re: obsah stvorca
↑ jozotom:, ↑ Cheop:
A jo, děkuji a omlouvám se, tu chybu jsem opravdu přehlédl (o řádek výše to má ↑ jozotom: ještě dobře).
EDIT: Napadlo mne podívat se na papír, kde jsem to před tím pčítal, a tam to mám dobře, takže pro dnešek bych toho měl
asi už nechat.
Ale od začátku mám dojem, že je špatně ta druhá rovnice nepozorným umocněním dvojčlenu.
Strana BC má délku  ,
,
výraz  pro délku straany AB je správně. Odtud správná rovnice
pro délku straany AB je správně. Odtud správná rovnice 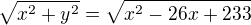 , neboli
, neboli  .
.
Celkem jsme tedy měli získat soustavu  ,
,  .
.
Ale jak ji řešit nějak inteligentně, to mne bohužel zatím nenapdá. :-(
Offline
#10 22. 04. 2011 16:41
Re: obsah stvorca
↑ jozotom:
"Syntetické" řešení je následující:
Označme P počátek soustavy , E kolmý průmět bodu C na osu x.
Potom trojúhelníky PBA, ECB jsou shodné podle věty usu (kde "s" = BA = CB).
Takže x = |PB| = |EC| = 8 , y = |AP| = |BE| = 13 - x = 13 - 8 = 5 ,  .
.
Offline
#12 22. 04. 2011 19:21 — Editoval Dana1 (22. 04. 2011 19:23)
- Dana1
- Host
Re: obsah stvorca
↑ jozotom:
Trojuholníky PBA a ECB sú zhodné.
Dĺžka PB je taká istá ako dĺžka CE a pretože dĺžka CE je určená ypsilonovou súradnicou bodu C, jej hodnota je 8.
AP má dĺžku rovnakú ako BE. Pretože bod E leží v xovej súradnici bodu C, jeho vzdialenosť od P je 13. PB má dĺžku 8 (ako je ukázané vyššie),
vzdialenosť BE je 13 - 8, čo je 5. Táto vzdialenosť je podľa zhodnosti trojuholníkov rovná aj dĺžke AP.
#13 23. 04. 2011 11:05 — Editoval Rumburak (23. 04. 2011 11:31)
Re: obsah stvorca
↑ jozotom:
Pokud to ani teď není zcela jasné, vysvětlím to ještě z trochu jiného pohledu.
Zakresli si body P[0,0], E[13,0], F[13,13], G[0,13] .
Obrazec PEFG je čtverec, na jehož straně EF leží daný bod C. Dále: na straně GP má ležet bod A a na straně PE má ležet bod B.
Bod M[13/2, 13/2] je zřejmě středem úsečky PF, která je úhlopříčkou čverce PEFG, takže M je středem tohoto čtverce.
Nechť nyní f představuje otočení se středem v bodě M a úhlem 90 st. v záporném smyslu (tj. po směru hodinových ručiček).
Při tomto otočení se úsečka EF zobrazí na ús. PE, ús. PE na GP, ús. GP na FG a ús. FG na EF.
Chceme-li do čtverce PEFG vepsat čtverec podle našeho zadání, můžeme postupovat tak, že na daný bod C (ležící na ús. EF)
budeme iteračně (=postupně) aplikovat otočení f. Získáme tak body B = f(C) na straně PE, A= f(B) na str. GP , D = f(A) na str. FG .
Další otočení dává C = f(D), čímž se lomená čára uzavře a vznikne tak čtverec ABCD podle zadání úlohy. Plyne to z elementárních
vlastností čtverce (ABCD): obě jeho úlopříčky jsou stejně dlouhé, navzájem se půlí a jsou na sebe kolmé. Ze skutečnosti, že i PEFG
je čtverec, vyplývá, že jiný čtverec ABCD (splňující tadání) než ten, který jsme získali výše uvedeným postupem, neexistuje.
Otočení je shodné zobrazení, takže úečka PB, která je obrazem úcečky EC při otočení f, má stejnou délku jako ús. EC, tedy délku 8.
Takže B = [8, 0], |BE| = 13 - 8 = 5. Z Pythagorovy věty pro prvoúhlý trojúh. BEC vypočítáme druhou mocninu jeho přepony BC,
což je zároveň obsah čtverce ABCD.
Offline
#15 26. 04. 2011 09:40 — Editoval Rumburak (26. 04. 2011 09:54)
Re: obsah stvorca
Ještě dotáhněme do konce to analytické řešení.
Zrekapitulujme, že je dán bod C[13, 8], k němuž máme nelézt body A[0, y] , B[x, 0] tak, aby
(1) (A - B)(C - B) = 0 .... kolmost úseček AB, CB ,
(2) |A - B| = |C - B| .... shodnost úseček AB, CB .
(Po nalezení bodů A, B bude zbývající bod D čtverce ABCD určen vztahem D - A = C - B .)
Podmínky (1), (2) vedou k rovnicím
(1a)  ,
,
(2a)  .
.
Postup jejich řešení je poněkud nestandardní: rovnici (2a) vynásobíme  , obdržíme
, obdržíme

a sem dosadíme  dle (1a). Výslednou rovnicí bude
dle (1a). Výslednou rovnicí bude
 ,
,
kterou dále upravujeme :
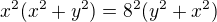 ,
,
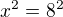 (dělit předchozí rovnici výrazem
(dělit předchozí rovnici výrazem  bylo korektní, protože dle (2a) je nenulový),
bylo korektní, protože dle (2a) je nenulový),
 ,
,
odtud a z (1a)  .
.
Máme tedy dva čtverce, které úloze vyhovují. Snadno dopočítáme jejich obsahy: 89 resp. 505.
EDIT. Tato úloha demonstruje užitečnost analytické geometrie, neboť jejími metodami vyplavou na povrch i taková řešení,
která nebijí do očí .
Offline
#16 26. 04. 2011 10:46
#18 26. 04. 2011 11:16
Re: obsah stvorca
↑ Cheop:
Děkuji za pěkné doplnění.
Připojuji se k dotazu kolegy ↑ Jenda358:, ovšem pouze v případě, že nejede o "výrobní tajemstvi" :-) .
Offline
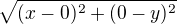 BA
BA BC
BC BA
BA BC
BC