Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#276 06. 12. 2009 18:13
#277 06. 12. 2009 18:22
#278 13. 12. 2009 09:21
#279 13. 12. 2009 09:31
Re: Lomené výrazy
u toho prvního nemáš exponenty (resp. v exponentu nemůže být "=")
jinak postup je asi takový, že roznásobíš závorku (podle vzorce (A-B)^2, tedy jestli v exponentu má být 2), pak posčítáš to, co sečíst můžeš (předpokládám, že to první p^ má být taky p^2 -> pak by se dali sečíst ta p^2; a zároveň můžeš 15 přehodit na levou stranu rovnice); pak řešíš jako kvadratickou rovnici..
2) x.(x-2)+5+4x=(x+1)(x-3)
postup - roznásob závorky, posčítej, vše si přesuň na jednu stranu rovnice a pak vyřeš jako kvadratickou rovnici
3)
obě strany rovnice vynásob 4 (největší jmenovatel), posčítej, co sčítat můžeš, dále řeš jako lineární rovnici.
Zkus sem napsat své řešení, já (resp. někdo jiný) ti to jistě zkontroluje
Offline
#280 13. 12. 2009 09:35 — Editoval FailED (13. 12. 2009 21:33)
Re: Lomené výrazy
↑ MICHAL B:
Co to znamená p^ ? Myslíš druhou mocninu? To se píše p^2
Edit: nejdřív to zkus podle postupu ↑ Doxxik:
Offline
#281 13. 12. 2009 10:03
Re: Lomené výrazy
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#282 13. 12. 2009 20:18
Re: Lomené výrazy
↑ Doxxik:
p^2-(p-5)^2=15
p^2-p^2-10p+25=15
10p=-10 /10
p=-1
x*(x-2)+5+4x=(x+1)*(x-3)
x^2-2x+5+4x=x^2-3x+x-3
x^2-x^2-2x-4x+3x-x=-3-5
-4x=-8 /-4
x=2
x + x+2 - x-3 =3 /4
------ -----
2 4
4x+(2x+4)-(x-3)=12
4x+2x+4-x+3=12
4x+2x-x = 12-7
5x = 5 /5
x=1
tak jsem to tady zkusil spočítat tak mi to prosím zkontroluj a napis jak to vyslo tobě dík M.
Offline
#283 13. 12. 2009 21:16
Re: Lomené výrazy
↑ MICHAL B:
p^2-(p-5)^2=15
p^2-p^2-10p+25=15
10p=-10 /10
p=-1
Je špatně. Pokud máš mínus před závorkou musíš změnit při odstraňování té závorky všechny znaménka...ty si změnil akorát to první u p^2.
Offline
#284 13. 12. 2009 21:20 — Editoval septolet (13. 12. 2009 21:25)
Re: Lomené výrazy
↑ MICHAL B:
x*(x-2)+5+4x=(x+1)*(x-3)
x^2-2x+5+4x=x^2-3x+x-3
x^2-x^2-2x-4x+3x-x=-3-5
-4x=-8 /-4
x=2
Správný výsledek je x = -2. Ještě druhý řádek je správně, pak si se v tom ztratil.
EDIT: Třetí příklad máš správně.
Offline
#285 08. 01. 2010 13:17
- hofmanova.darina
- Příspěvky: 49
- Reputace: 0
Re: Lomené výrazy
Zdravím všechny a prosím o pomoc při řešení tohoto problému:
Zjednodušte lomený výraz a určete podmínky platnosti:x na druhou - x lomeno x - 1 =
vůbec nechápu co se po mě chce.Všem moc díky Darča
Offline
#286 08. 01. 2010 13:37 — Editoval gladiator01 (08. 01. 2010 13:40)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Lomené výrazy
↑ hofmanova.darina:
Založ si vlastní téma a zkopíruj do něj toto zadání viz. pravidla. Sem pak dej na něj odkaz.
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#287 08. 01. 2010 13:38
Re: Lomené výrazy
↑ hofmanova.darina: Příště si prosímtě založ nové téma, protože takto by to také nemusel nikdo najít a nedočkala by ses odpovědi. za předpokladu, že jsem mohl krátit, tedy že to, čím jsem krátil, nebyla nula, tedy za předpokladu, že
za předpokladu, že jsem mohl krátit, tedy že to, čím jsem krátil, nebyla nula, tedy za předpokladu, že  .
.
Offline
#288 13. 06. 2010 21:59
- Filip Novotný
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Lomené výrazy
Dobrý den, jsem tu nový a chtěl bych se zeptat, zda by mi někdo mohl pomoci s tímto příkladem, pomocí použití (-1) ve jmenovateli a poté i při samotném počítání. Abych tomu dobře rozuměl. Děkuji moc.
Offline
#289 13. 06. 2010 22:19
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Lomené výrazy
↑ Filip Novotný:
Založ si vlastní téma a zkopíruj do něj toto zadání viz. pravidla. Sem pak dej na něj odkaz s poznámkou.
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#290 13. 06. 2010 22:21
#292 13. 06. 2010 23:01
- Filip Novotný
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Lomené výrazy
gadgetka napsal(a):
nebo si můžeš nejdřív upravit zlomky na:
Díky, teďka jsem pokročil v tom, jak jsi psala tu úpravu zlomků a vyšlo mi tohle, ale když chci pokročit dál tak to takhle evidentně bude špatně:
Offline
#293 13. 06. 2010 23:04
Re: Lomené výrazy
1 musíš převést také na společného jmenovatele, takže získáš zlomek  a přičteš ho k tebou upravenému zlomku (máš ho upravený správně)
a přičteš ho k tebou upravenému zlomku (máš ho upravený správně)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#294 13. 06. 2010 23:12 — Editoval Filip Novotný (13. 06. 2010 23:13)
- Filip Novotný
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Lomené výrazy
gadgetka napsal(a):
1 musíš převést také na společného jmenovatele, takže získáš zlomek
a přičteš ho k tebou upravenému zlomku (máš ho upravený správně)
Promiň, ale nějak ti nerozumím, co přesně mám s tou 1 udělat?
Offline
#295 13. 06. 2010 23:27
Re: Lomené výrazy
Když k zlomku přičítáš 1, musíš ji převést na společného jmenovatele. Když máš např.  Společným jmenovatelem bude
Společným jmenovatelem bude 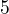 a v čitateli dostáváš
a v čitateli dostáváš  ; jedničku sis prostě v tomto případě představil jako
; jedničku sis prostě v tomto případě představil jako  .
.
V našem příkladě je společným jmenovatelem všech zlomků výraz (b-3)(b+3), takže jedničku si tím pádem představíš jako 
A sčítáš:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#296 13. 06. 2010 23:36 — Editoval Filip Novotný (13. 06. 2010 23:36)
- Filip Novotný
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Lomené výrazy
jo takhle, to by mě nenapadlo, tak moc díky, zase jsem o kus dál.
Offline





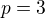



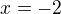





.jpg)



