Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 05. 2011 19:54
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: dělitelnost polynomů
Dle mého ano:
Předpokládejme, že tomu tak není. Pak je zřejmě stupeň Q aspoň 1. Víme, že existují polynomy R,S, že P=Q.R+S, kde stupeň S < stupeň Q (*). Pokud Q(n) dělí P(n), pak musí i Q(n) dělit S(n). Tedy pro všechna n Q(n) dělí S(n). Tedy existuje dostatečně velké n0, že abs(Q(n0))>abs(S(n0)) (dle (*)) a Q(n0) i S(n0) <> 0. Pak nemůže Q(n0) dělit S(n0).
"Máte úhel beta." "No to nemám."
Offline
#3 02. 05. 2011 21:44 — Editoval check_drummer (02. 05. 2011 22:09)
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: dělitelnost polynomů
↑ OiBobik:
To je pravda, obecně budou mít R,S racionální koeficienty. Pro vhodné m přirozené lze však dosáhnout vztahu m.P=Q.R.m+S.m, kde R.m a S.m jsou celočíselné polynomy.
Pokud se nám podaří ukázat, že Q nedělí m.P, pak jsme hotovi (použijeme argument výše). Zkusím se nad tím zamyslet.
Edit: Předpokládejme pro spor opak, tedy, že Q dělí m.P, tedy že P je tvaru Q.A/m pro nějaký polynom A. Potom pro každé n m dělí A(n). Pokusme se ukázat, že z toho plyne, že A je tvaru m.B pro nějaké B. Pak totiž bude P tvaru Q.B a tedy Q dělí P, což je spor.
Tedy zbývá dokázat: Pokud pro každé n platí, že m dělí A(n) (A je polynom s celočíselnými koeficienty), pak A=m.B pro nějaký polynom B. (To je speciální případ věty dokazované.)
Více snad zítra.
"Máte úhel beta." "No to nemám."
Offline
#4 03. 05. 2011 11:09 — Editoval musixx (03. 05. 2011 11:57)
Re: dělitelnost polynomů
Jen bych doformalizoval již napsané...
Nikde se nepíše, nad jakým okruhem jsou polynomy konstruovány, ale dá se předpokládat, že to bude alespoň  , tedy
, tedy ![kopírovat do textarea $P,Q\in{\mathbb Z}[x]$](/mathtex/19/194f8e57a38f67c01cb1dd8e2aa12bdd.gif) , případně
, případně ![kopírovat do textarea ${\mathbb Q}[x]$](/mathtex/75/7563f90aaeb44ed8fcba249c16189f2d.gif) ,
, ![kopírovat do textarea ${\mathbb R}[x]$](/mathtex/cd/cd1c83ddaa1fd00ed14ee46c80857086.gif) ,
, ![kopírovat do textarea ${\mathbb C}[x]$](/mathtex/06/0675f245d6aeb0d265363e74b2d9f64e.gif) . Ale to nás ani nijak zajímat nemusí. Předpokládejme tedy přirozeně, že jsou nad okruhem charakteristiky 0 obsahujícím celá čísla.
. Ale to nás ani nijak zajímat nemusí. Předpokládejme tedy přirozeně, že jsou nad okruhem charakteristiky 0 obsahujícím celá čísla.
Kdyby byl Q nulový polynom, pak protože nula dělí pouze nulu, a protože nenulový polynom P nemůže mít nekonečně mnoho kořenů (všechna přirozená čísla), pak i samo P je nula a tvrzení platí.
Dále tedy předpokládejme nenulové Q.
Jistě vždy pak lze psát  pro vhodné
pro vhodné  a R(x) a S(x) s celočíselnými koeficienty. Můžeme přidat navíc požadavek, aby
a R(x) a S(x) s celočíselnými koeficienty. Můžeme přidat navíc požadavek, aby  s obvyklou konvencí
s obvyklou konvencí  .
.
Q je nenulový, a tedy pro všechna x větší než největší (reálný) kořen polynomu  je polynom Q(x) monotónní, proto existuje takové přirozené
je polynom Q(x) monotónní, proto existuje takové přirozené  , že posloupnost
, že posloupnost 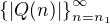 je rostoucí posloupnost přirozených čísel. Stejně tak pro polynom S(x). No a z porovnání stupňů Q a S plyne existence přirozeného
je rostoucí posloupnost přirozených čísel. Stejně tak pro polynom S(x). No a z porovnání stupňů Q a S plyne existence přirozeného 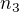 takového, že
takového, že  pro všechna přirozená
pro všechna přirozená  .
.
Protože ale  je pro přirozené x rovnost v celých číslech a protože tvrdíme, že Q(n) dělí P(n) pro všechna přirozená n, pak také Q(n) musí dělit S(n) pro všechna přirozená n, tedy zejména pro ta větší než
je pro přirozené x rovnost v celých číslech a protože tvrdíme, že Q(n) dělí P(n) pro všechna přirozená n, pak také Q(n) musí dělit S(n) pro všechna přirozená n, tedy zejména pro ta větší než 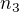 . Těch je ale nekonečně mnoho a současně pro všechna z nich platí
. Těch je ale nekonečně mnoho a současně pro všechna z nich platí  , tedy jediná možnost je, že pro všechna tato n je S(n) rovno nule.
, tedy jediná možnost je, že pro všechna tato n je S(n) rovno nule.
Ovšem nenulový nemůže mít nekonečně mnoho kořenů, tedy S(n) musí být nulový polynom, což dokazuje, že polynom  dělí polynom
dělí polynom 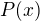 , ať už byly polynomy P a Q konstruovány nad jakýmkoli okruhem obsahujícím celá čísla.
, ať už byly polynomy P a Q konstruovány nad jakýmkoli okruhem obsahujícím celá čísla.
Offline
#5 03. 05. 2011 18:20
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: dělitelnost polynomů
↑ musixx:
Ano, je to tak, klíčový bod, že Q(n) dělí S(n) mě také dnes napadl. Zbytek plyne z toho, že stupeň Q > stupeň S, přesně tak, jak píšeš.
"Máte úhel beta." "No to nemám."
Offline
#7 29. 01. 2019 15:10
#9 29. 01. 2019 20:40
Re: dělitelnost polynomů
↑ Pavla11:
Ahoj, neni to spravne. Pokud a=1,c=1 a b=-2, potom  .
.
My ale chceme  a
a  .
.
Z druhe rovnice vyplyva, ze  . Dosazenim do prvni rovnice ziskame
. Dosazenim do prvni rovnice ziskame , takze
, takze  a
a 
Cemu se musi rovnat  , aby
, aby  i
i  byla cela cisla? (jsou 2 moznosti)
byla cela cisla? (jsou 2 moznosti)
Offline



