Matematické Fórum

allstar

Ahoj,
potreboval bych pomoct s timto prikladem:

$\sum 2^{n(x+6)}$
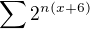
a) Konverguje rada STEJNOMERNE na intervalu konvergence?
b) Konverguje rada STEJNOMERNE na intervalu <-100;-50> ?

Dik moc.

Jediny co zatim vim, je ze interval bodove konvergence je (-oo; -6)

Saturday · 25. 05. 2008 18:46

↑ allstar:

EDIT: SPATNE JSEM PRECETL ZADANI A RESIL JAKO POSLOUPNOST FUNKCI A NE FUNKCI RADY

na zacatek bych zavedl znaceni:
$f_n(x) = 2^{n(x+6)}$
$f(x) = \lim \limits_{n \to \infty} 2^{n(x+6)} = 0$ pro $x \in (-\infty, -6)$

a) Toto je nutna a postacujici podminka stejnomerne konvergence:

$\lim_{n \to \infty} \sup \limits_{x \in (\text{vysetrovany interval})} | f_n(x) - f(x)| = 0$ ... kde sup oznacuje supremum

V nasem pripade:

$\lim_{n \to \infty} \sup \limits_{x \in (-\infty, -6)} | 2^{n(x+6)} - 0 | = 1$ (pro pevne n hledas takove x, ze vyraz v absolutni hodnote bude maximalni => "budes se blizit k -6 zleva" osklive receno a dostanes pro libovolne n hodnotu suprema 1.

Zaver: na intervalu (-oo, -6) rada konverguje pouze lokalne stejnomerne (kdyz si vyberes libovolny bod z intervalu (-oo,-6), tak v okoli tohoto bodu bude rada konvergovat stejnomerne)

b) ano, na tomto intervalu rada konverguje stejnomerne

Obrazek
=========

Zde jsou na osklivem obrazku znazorneny prubehy jednotlivych funkci f_n (pro rostouci n funkce f_n rostou pomaleji, tzn. ta modra fce je f_1 a ta funkce, ktera uz temer kopiruje osu x je f_20)

Doufam, ze pomohlo, pokud vidis nejakou chybu, tak mi dej pls vedet.

xificurC · 25. 05. 2008 23:27

↑ Saturday:
Len pre istotu, mari sa mi, ze supremove kriterium, ktore si napisal, sa zavadza a pouziva pri postupnostiach, toto je vsak rad a pri nom sme sa my osobne ucili lim sup |sn_x - s_x| , teda limita suprema suctu radu a toho, k comu sucet konverguje... Nebude v tom nejaky rozdiel??

Saturday · 25. 05. 2008 23:37

↑ xificurC: Mas pravdu, je to o posloupnostech funkci a v zadani jsou rady. Jen nevim, jestli to mam mazat nebo ne, psal jsem to docela dlouho (i kdyz zbytecne :-)).

Marian · 26. 05. 2008 10:17

Mozna by mohlo pomoct toto

$2^{n(x+6)}=\left (2^{x+6}\right )^n.$

Matematické Fórum

#1 25. 05. 2008 17:52 — Editoval allstar (25. 05. 2008 18:00)

Stejnomerna konvergence funkcni rady

#2 25. 05. 2008 18:46

Re: Stejnomerna konvergence funkcni rady

#3 25. 05. 2008 23:27

Re: Stejnomerna konvergence funkcni rady

#4 25. 05. 2008 23:37

Re: Stejnomerna konvergence funkcni rady

#5 26. 05. 2008 10:17

Re: Stejnomerna konvergence funkcni rady

Zápatí