Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » definite integral (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 05. 2011 04:00
- stuart clark

- Příspěvky: 1015
- Reputace: 7
definite integral
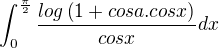
Offline
- (téma jako vyřešené označil(a) byk7)
#2 13. 05. 2011 12:00
Re: definite integral
↑ stuart clark:
I managed to prove that the integral equals to
The proof is quite difficult, so I write it here later.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 14. 05. 2011 15:09 — Editoval Marian (04. 09. 2013 00:13)
Re: definite integral
↑ stuart clark:
I think, my solution uses probably different steps as in Pavel's case because the form of my final result is more simple. We prove the following equality
Offline
#4 14. 05. 2011 16:38
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: definite integral
Thanks to Paul and Marian.(for crystal clear explanation).
Offline
#5 16. 05. 2011 19:38 — Editoval Pavel (16. 05. 2011 19:42)
Re: definite integral
↑ Marian:
Marian, it is a very nice solution using elementary tools of calculus. My solution is more difficult. It is based on the expressing of the logarithmic function by differentiation and integration of an infinite series and on the solving of a linear differential equation of the first order in a special form.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 17. 05. 2011 04:51
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: definite integral
Paul very Nice Solution Using Power Series but Complex to understand.
anyway again Thanks for Nice Solution.
Offline
#7 17. 05. 2011 15:50
Re: definite integral
↑ Pavel:
Napadlo mě řešit podobně jako ty. Ale vzpomněl jsem si, že tyto integrály se hezky dají řešit pomocí dvojných integrálů a Fubiniho věty (Myslím, že nějaká drobná poznámka bude i v Jarníkově Integrálním počtu II).
I když mám výsledek ve snažším tvaru, tvůj postup chápu jako zajímavou výstavku vybraného matematického chování (řekněme, bonton vyšší matematické společnosti). Nejvíce mě ovšem dostalo, že sčítáš nekonečnou potenční řadu prostřednictvím nehomogenní lineární difereniální rovnice. Docela poučná manipulace.
Bravo!
Offline
#8 17. 05. 2011 16:24 — Editoval Pavel (17. 05. 2011 16:24)
Re: definite integral
↑ Marian:
Tuším, že něco podobného je ve Knoppovi - Theory and Application of Infinite Series. Taky tam sčítá potenční řady tak, že vytvoří derivováním a integrováním vztah mezi hledaným součtem a jeho derivacemi. Na toho Jarníka se podívám, Tvoje metoda vypadá dost chutně a výživně.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » definite integral (TOTO TÉMA JE VYŘEŠENÉ)

 . In virtue of the periodicity of the cosine-function we can consider only the case
. In virtue of the periodicity of the cosine-function we can consider only the case ![kopírovat do textarea $\alpha\in (-\pi ,\pi]$](/mathtex/de/de228c11e183ec70b7142306421d4a42.gif) . Also, denote the given integral as follows:
. Also, denote the given integral as follows:![kopírovat do textarea $
I(\alpha ):=\int_{0}^{\pi /2}\frac{\ln (1+\cos (\alpha)\cdot\cos (x))}{\cos (x)}\mathrm{d}x,\qquad \alpha\in (-\pi ,\pi].
$](/mathtex/c7/c7681ab388a16382abfa07bf95045008.gif)



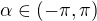 we have
we have


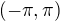 . It is possible to show that for
. It is possible to show that for  the derived result holds also true. This finishes the proof of the desired identity.
the derived result holds also true. This finishes the proof of the desired identity.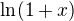 :
:
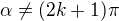 and
and ![kopírovat do textarea $x\in[0,\pi/2]$](/mathtex/61/61ff93ae546eb75456d862bcf80ea9cd.gif) . Then
. Then  and we can write that
and we can write that
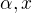 . Therefore it can be integrated, thus
. Therefore it can be integrated, thus
 -st power of the cosine function (
-st power of the cosine function (
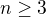 is even then
is even then![kopírovat do textarea $
\int_{0}^{\frac{\pi}{2}}(-1)^{n+1}\frac{\cos^{n}\alpha\cdot\cos^{n-1}x}{n}\,\text{d}x
&=-\frac{\cos^{n}\alpha}n\int_{0}^{\frac{\pi}{2}}\cos^{n-1}x\,\text{d}x\\
&=-\frac{\cos^{n}\alpha}n\left(\[\frac{\cos^{n-2}x\cdot\sin x}{n-1}\]_{0}^{\frac{\pi}{2}}+\frac{n-2}{n-1}\int_{0}^{\frac{\pi}{2}}\cos^{n-3}x\,\text{d}x\right)\\
&=-\frac{\cos^{n}\alpha}n\cdot\frac{n-2}{n-1}\int_{0}^{\frac{\pi}{2}}\cos^{n-3}x\,\text{d}x
=\dots\\
&=-\frac{\cos^{n}\alpha}n\cdot\frac{n-2}{n-1}\cdot\frac{n-4}{n-3}\dots\frac{2}{3}\int_{0}^{\frac{\pi}{2}}\cos x\,\text{d}x
=\,{\color{blue}-\frac{\cos^{n}\alpha}n\cdot\frac{n-2}{n-1}\cdot\frac{n-4}{n-3}\dots\frac{2}{3}}
$](/mathtex/4f/4f98e47c854cf8a78919e17a4b265e9a.gif)

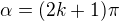 and
and ![kopírovat do textarea $x\in[\delta,\pi/2]$](/mathtex/94/94d33203074e8c62d7c7ee80298da50d.gif) with
with  then
then  and
and

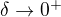 . We derive from it that the blue idenitites hold true also in this case, i.e. for
. We derive from it that the blue idenitites hold true also in this case, i.e. for 


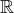 .
.  . First, we derive it and then we use the binomial theorem for a real exponent (
. First, we derive it and then we use the binomial theorem for a real exponent (
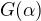 .
.
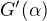 as in the previous case. Let us define an auxilary function
as in the previous case. Let us define an auxilary function
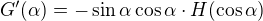 . We will derive a special linear differential equation such that its solution is just the function
. We will derive a special linear differential equation such that its solution is just the function 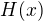 .
. 


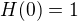 we deduce that
we deduce that 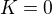 . Thus
. Thus
