Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » real roots (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 05. 2011 04:31
- stuart clark

- Příspěvky: 1015
- Reputace: 7
real roots
Prove That the equation  has all Real roots.
has all Real roots.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 17. 05. 2011 12:38 — Editoval Pavel (17. 05. 2011 12:42)
Re: real roots
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 17. 05. 2011 18:26
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: real roots
↑ stuart clark:
It has to be said from what number set the values a-h,k,A-H are, I suppose they are real numbers, aren't?
"Máte úhel beta." "No to nemám."
Offline
#4 23. 05. 2011 09:21
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: real roots
thanks Paul for Nice solution.
and check_drummer you are saying Right.
Offline
#5 23. 05. 2011 12:47 — Editoval musixx (23. 05. 2011 13:43)
Re: real roots
Let's use 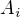 instead of A,B,C, ..., and let's use
instead of A,B,C, ..., and let's use  instead of a,b,c, ... .
instead of a,b,c, ... .
Then we are looking for zeroes of a function 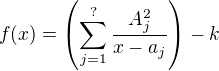 . As Pavel has remarked, all the possible roots are also roots of some polynomial with real coefficients, so all its roots are realized within complex numbers.
. As Pavel has remarked, all the possible roots are also roots of some polynomial with real coefficients, so all its roots are realized within complex numbers.
So what is 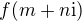 ? The imaginary part clearly is
? The imaginary part clearly is 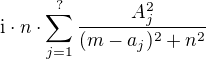 , so the sum cannot be zero (EDIT: if at least one of A_i and one of a_i are nonzero which is a natural assumption), and since we are looking for
, so the sum cannot be zero (EDIT: if at least one of A_i and one of a_i are nonzero which is a natural assumption), and since we are looking for 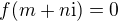 , we have n=0, so therefore only real roots.
, we have n=0, so therefore only real roots.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » real roots (TOTO TÉMA JE VYŘEŠENÉ)

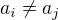 for
for 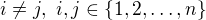 . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  .
.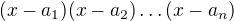 we get that
we get that
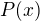 of degree
of degree  resp.
resp.  , if we consider that
, if we consider that  resp.
resp. 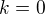 . All the roots of this equation are the roots of the former equation and vice versa. Show that there exist just
. All the roots of this equation are the roots of the former equation and vice versa. Show that there exist just 

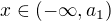 . Then the function
. Then the function  is decreasing and continous in
is decreasing and continous in 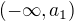 ,
, 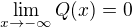 and
and 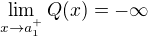 . From these facts it follows that
. From these facts it follows that 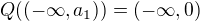 .
. then
then 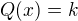 has no solution in
has no solution in  then
then 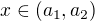 . Then the similar facts together with
. Then the similar facts together with 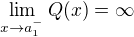 and
and 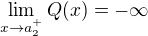 imply that
imply that 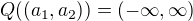 .
.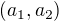 .
. 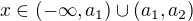 ,
,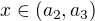 . Then the similar facts together with
. Then the similar facts together with 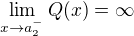 and
and 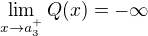 imply that
imply that 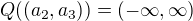 .
.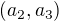 .
. 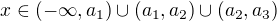 ,
,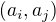 ,
, 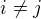 .
. 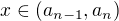 . Then the similar facts together with
. Then the similar facts together with 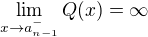 and
and 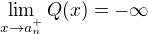 imply that
imply that 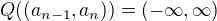 .
.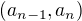 .
. 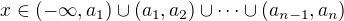 ,
,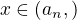 . Then the similar facts together with
. Then the similar facts together with 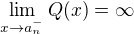 and
and 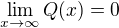 imply that
imply that 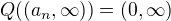 .
.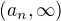 ,
,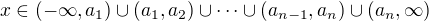 ,
,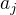 are pairwise distinct. If there exist
are pairwise distinct. If there exist  such that
such that 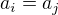 then
then 