Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 17. 05. 2011 21:44

Vlastik
Příspěvky: 40
Reputace:   0 
 

Exponenciální nerovnice

Dobrý večer, mám tu opravdovou lahůdku, mohl by mi někdo prosím spočítat nejtěžší nerovnici všech dob ?

(1/16)^x > 1

Řešením této nerovnice jsou právě všechna x (R), pro něž platí : měl by to být interval (-nekonečo, 0)

Offline

 

#2 17. 05. 2011 21:52

jrn
Příspěvky: 398
Reputace:   11 
 

Re: Exponenciální nerovnice

Zdravím, nepomohlo by nakreslit graf?

Offline

 

#3 17. 05. 2011 21:53

Aquabellla
Moderátorka Bellla
Místo: Brno
Příspěvky: 1473
Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
Pozice: Absolventka Bc., studentka NMgr.
Reputace:   98 
 

Re: Exponenciální nerovnice

↑ Vlastik:
Co je na ní superpřetěžkého?

$(1/16)^x > 1^0$
$16^x < 1^0$
$x < 0$

Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.

Offline

 

#4 17. 05. 2011 21:54 — Editoval Dana1 (17. 05. 2011 21:54)

Dana1
Host
 

Re: Exponenciální nerovnice

↑ Vlastik:

Dobrý večer. Mohol by si sformulovať problém, ktorý máš s úlohou? (Pravidlá)

 

#5 17. 05. 2011 21:58 — Editoval miso16211 (18. 05. 2011 12:38)

miso16211
Πυθαγόραc
Příspěvky: 1522
Pozice: n/a
 

Re: Exponenciální nerovnice

Nechcem sa chvalit ale ja som to dal v hlave.
1. x=0 priesecnik grafov funckii y=1 a 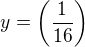$y=\(\frac1{16}\)$
2,viem ze 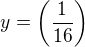$y=\(\frac1{16}\)$ klesa a kedy je vacsi? Ked (-nekonecno,0)

https://dobramatematika.blogspot.com

Offline

 

#6 17. 05. 2011 22:36

Vlastik
Příspěvky: 40
Reputace:   0 
 

Re: Exponenciální nerovnice

Jak prosímtě funguje ta 1^0, když sní operuješ ? podle vzorce by to mělo mít stejný základ ty dvě strany nerovnice. Potřebuju vědět jak jsi odůvodnil že 16 je to samé jako 1^0.

Offline

 

#7 17. 05. 2011 22:37

Vlastik
Příspěvky: 40
Reputace:   0 
 

Re: Exponenciální nerovnice

↑ Dana1: Nevím jak ji spočítat.

Offline

 

#8 17. 05. 2011 22:42 — Editoval Dana1 (17. 05. 2011 22:49)

Dana1
Host
 

Re: Exponenciální nerovnice

↑ Vlastik:

Vlastík, ale to je úloha z definície, úplne základná...

Vidíš, tú jednotku si si všimol, niečo vieš... Ako sa Ti má pomôcť, keď nepovieš, čomu nerozumieš?

Asi to bolo myslené takto... :

$16^x < 16^0$

Ešte musíš vedieť, či graf rastie alebo klesá - preto tá poznámka od jrn. (Či pre menšie čísla v exponente sa vyrátajú aj menšie hodnoty mocnín.)

To vyplýva z hodnoty základu, myslím...

 

#9 17. 05. 2011 22:47

Vlastik
Příspěvky: 40
Reputace:   0 
 

Re: Exponenciální nerovnice

↑ Dana1: Mno a ani to nebolelo :)) díky, tohle jsem si potřeboval uvědomit, jisté základní matematické definice mi unikají stím nic nenadělám :) díky moc

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson