Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » no. of real solution (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 05. 2011 05:00
- stuart clark

- Příspěvky: 1015
- Reputace: 7
no. of real solution
Maximum number of real solution of the equation 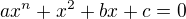 Where
Where 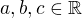 and
and 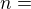 even positive Integer.
even positive Integer.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 26. 05. 2011 10:03 — Editoval musixx (26. 05. 2011 10:07)
Re: no. of real solution
Let's investigate local extrems of a function 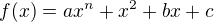 , and let's assume a nontrivial case
, and let's assume a nontrivial case  and even.
and even.
Its first derivative is 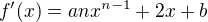 .
.
A degree of a polynomial 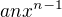 is odd. Therefore there can be only one intersection with a line
is odd. Therefore there can be only one intersection with a line 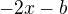 for positive
for positive  , and up to three intersections with a negative
, and up to three intersections with a negative  . A case of positive
. A case of positive  is therefore not interesting, since it can lead only up to two real roots of
is therefore not interesting, since it can lead only up to two real roots of  .
.
If we further analyze the second derivative 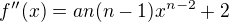 (
( negative), we can see that we can have a sequence (from left to right on axis x) local maximum -- local minimum -- local maximum which could mean four roots (one in each of four invervals determined by zeroes of
negative), we can see that we can have a sequence (from left to right on axis x) local maximum -- local minimum -- local maximum which could mean four roots (one in each of four invervals determined by zeroes of 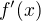 ).
).
In the same time this situation is achievable which is proven via a polynomial 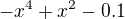 (clearly a maximum of
(clearly a maximum of 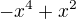 is 1/4, and it touches axis x in zero, therefore the subtraction of 0.1 which is somewhere between 0 and 1/4).
is 1/4, and it touches axis x in zero, therefore the subtraction of 0.1 which is somewhere between 0 and 1/4).
Final answer: such a polynomial can contain up to four real roots.
Offline
#3 27. 05. 2011 09:34
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: no. of real solution
Thanks musixx. very nice explanation.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » no. of real solution (TOTO TÉMA JE VYŘEŠENÉ)